Game Theory with Applications to Finance and Marketing I, Lecture 6 Notes (Oct. 27)
Game Theory with Applications to Finance and Marketing I, Lecture 6 Notes (Oct. 27)
Continue to Lecture 5, we shall still work on dealing with all sorts of games.
Bertrand Game
在Bertrand Game中,同样存在两个公司,生产同质(Homo-geneous)商品,卖给同质的客户。
- Producing one unit of the good costs $c$, where $0 < c < 1$.
- Each consumer is willing to pay as much as 1 dollar to buy $1$ unit of good.
- The total population of consumers is $1$. (After normalized, think as a kind of portion).
The firm are competing in price. Consumers maximize consumer surplus and firms maximize profits.
We can assume A pure strategy Nash Equilibrium is $(p_1, p_2)$, where $p_i$ is the price chosen by firm $i$, $i = 1, 2$, where $p_i$ is the price chosen by firm 1 and firm 2. If two firm choose the same price, they will get same market share.
Show that there is a unique Nash Equilibrium (called the Bertrand Outcome) where $p_1 = p_2 = c$.
Solution of Bertrand Game
As we can see, select $(p_1, p_2)$ is like choosing two points on a real number axis. But we can only choose the number in $[c, 1]$. (If choose $p_i < c$, it is crazy that the cost is greater than sell price.)
Case 1, Choose $p_1 < p_2$
In this case, consumers will surely by products from firm 1, as they can get max consumer surplus.
$\Rightarrow$ 选择比对手高的价格是一个strictly dominated strategy。不应该被使用
由Case 1推理……
从Case1推理可以得出,必然会有$p_1 = p_2$。
Case 2, Choose $p_1 = p_2 > c$
如果双方选择大于$c$的价格,则一方可以通过降价一点点的方式(例如降价$\Delta p$),从而做到比另一方价格低,从而拿下所有的消费者。因此不可能出现$p_1 = p_2 > c$
由Case 2推理……
因此,最后的Solution是
\[p_1 = p_2 = c\]这就是所谓的 Bertrand Paradox 。
相当于提示我们,不同厂商之间的产品最好有差异化,否则payoff将会夸张到为0,无法获得任何收益。
Why not mixed strategy?
这是因为所获得的payoff function不是连续的。
Modified Bertrand Game
现在考虑一个更改的Bertrand Game。厂商推出了所谓的“买贵退差价策略”。即,如果在外面能买到更低的价格的商品,厂商将退还额外的差价。现在这个Game的变化将如何?
Solution to Modified Bertrand Game
先观察下面这个例子:
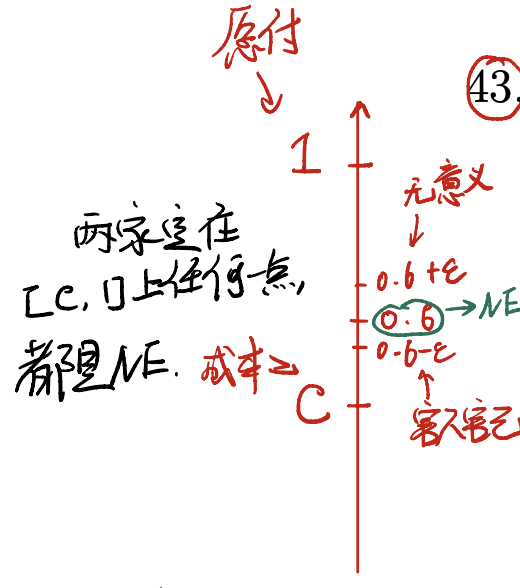
假设双方一开始都定在0.6的售价。
$1^{\prime}$ A公司提升售价到$0.6 + \epsilon$,此时由于买贵退差价策略,消费者还是会来购买,公司退掉差价即可。
$2^\prime$ A公司降价到$0.6-\epsilon$,由于买贵退差价,消费者还是可以去别人那里买,不会吸引到额外的消费者,反而让双方的利润降低。
因此在买贵退差价的前提下,提升价格是一个weakly donimate的策略,不但会让自己的payoff至少保持不变,反而还有可能升高。
在这种情况下,双方都会提升价格,最后到达消费者能接受的最高点,即到达$1$。
当然,在$[c, 1]$ 中的任意两点,也会是一个NE。
Non-homogeneous Products
现在来看非同质产品竞争的例子。
假设存在厂1和厂2,双方的需求函数分别为:
\[q_1 = 1 - p_1 + 0.5p_2\] \[q_2 = 1 - p_2 + 0.5p_1\]注意到两个厂商互相竞争。且双方产品的不同质在需求函数的系数中可以体现。同样,如果$p_1$不动,$p_2$上升,会让厂1的销量提升。
现在假设双方进行同时的价格竞争(即只改变价格,不改变产量,产量由需求决定)。
Solution to Non-homogeneous Products Game
对厂1而言,其目标是最大化利润。设其最好定价为$p_1^*$。
\[p_1^* = \arg\max_{p_1} p_1(1 - p_1 + 0.5p_2)\]同样地。记厂2最好定价为$p_2^*$,则有:
\[p_2^* = \arg\max_{p_2} p_2(1 - p_2 + 0.5p_1)\]通过求导的方式可以解得:
\[p_1^* = \frac {1 + 0.5p_2} {2}\] \[p_2^* = \frac {1 + 0.5 p_1} {2}\]双方互相猜忌,其实是一个递推式,最后将会收敛。即:
\(\lim_{n \rightarrow \infin} p_n = \frac {2} {3}\) 所以均衡时,双方各生产$2/3$单位的产品,定价为$2/3$。
Find SPNE (repeated game)
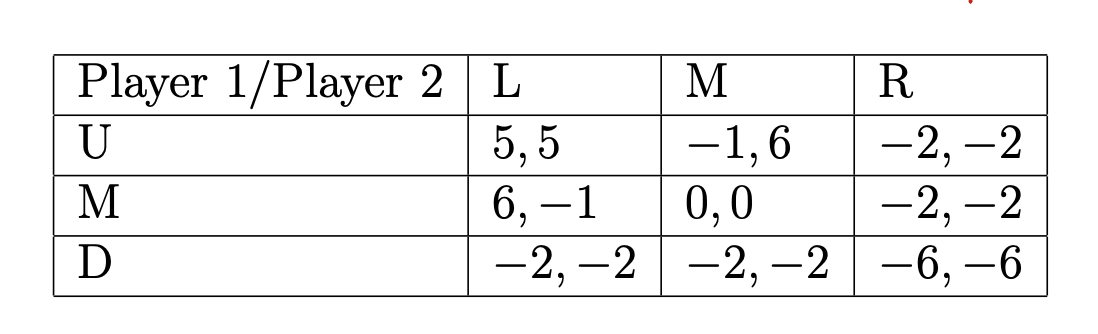
考虑下面这个game:
假如玩两轮,且为sequence game(可以看到对方第一轮出招),求NE?
Solution to SPNE
首先求第一轮的NE。
- 明显可以看到M是一个dominate strategy,所以Player2必定玩M。
- Player1此时只能也玩M。
- 因此,双方第一轮结束,NE为$(M, M)$。
再来看第二轮,同样的,假如player 1知道player 2必定玩M,他自己也没有什么好的办法。因为只有自己也出M,才能获得相应的收益。
因此,$(M, M)$不仅仅是一个NE,也是一个SPNE。
那么有没有其他的NE?考虑下面这个情况:
第一轮如果双方玩$(U, L)$且成功,首先会拿到$(5, 5)$的payoff。接下来会有:
- Player1使坏玩M,Player2猜到这种情况,他也会玩M。因此第二轮达成$(M, M)$的NE。
- Player2使坏玩M,同理也达成$(M, M)$的NE。
因此,第二个NE为:
\[(U, L) \rightarrow (M, M)\]注意这个只是NE,并非SPNE。
这个例子告诉我们,两阶段的Game与一阶段的Game是不相同的。需要谨慎识别与对待。
Forward Induction Game
下面我们来看Forward Induction Game这种赛局。考虑下面这个BoS Game:
- 在玩这个赛局前,Player1先选择去读书或者去演唱会。如果选择读书,则双方都会获得$(2, 2)$的payoff,游戏结束。
- 如果player1选择去演唱会,则会出现两种情况。双方喜欢不同的音乐(Bach与Stravinsky)
- 听Bach,得到$(3, 1)$
- 听Stravinsky,得到$(1, 3)$
- 如果不同,得到$(0, 0)$
Solution with Forward Induction Game
假如player1不选择读书,那一定是因为选择演唱会能拿到更高的payoff。
因此来看,player1一定希望双方一起听Bach(这样他得到3的收益,player2得到1的收益)。player2如果不从,双方都得到$(0, 0)$,还不如从了得到$(3, 1)$。
因此,最终双方选择$(B, B)$。
这就是一个典型的前向归纳,从对方的选择下手,才能找到如何出招。
probability Cournot Game
最后是一个带机率的古诺模型。
Reference
This note is mainly derived from Chyi-mei Chen’s Game Theory with Applications to Marketing and Finance, I Course @ National Taiwan University. Thanks him for giving this kind of excellent lecture.