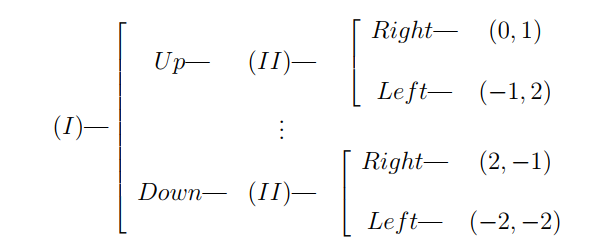Game Theory with Applications to Finance and Marketing I, Lecture 5 Notes (oct. 20)

Game Theory with Applications to Finance and Marketing I, Lecture 5 Notes (Oct. 20)

Subgame Perfect Nash Equilibrium (SPNE)

Definition of SPNE

A subgame perfect Nash equilibrium (SPNE) is an NE for a game in extensive form, which specifies NE strategies in each and every subgame.

用中文来说：

• 单独看每一个小赛局，如果大赛局的NE作用在每一个小赛局上，也能让这些小赛局达到NE，则这个大的NE就是SPNE。

Example of Solving SPNE

Game Tree and Extensive form of a game

Extensive form

A game can be described in extensive form, which needs to specify the timing of players’ moves and what they know when they move, in addition to the things specified in normal form. A game in extensive form is also known as an extensive game. Usually, a game in extensive form is depicted as a game tree.

简要来说，一个赛局的extensive form需要包括：

• timing：做动作的先后顺序
• information set：当player做动作的时候他们知道什么

经常用Game Tree来表述一个赛局的extensive form：

需要注意的是资讯集合这个概念。

Definition of Information Set: 一个赛局的资讯集合，在决策树中通常用圈来表示。圈内的东西都互相知道，圈外的东西并不清楚。

例如，在上图中，player I在他自己的资讯集合中，他不知道player II的资讯集合的动向。而player II的资讯集合也没有包括player I的动作。因此，他们都互相不知道对方做了什么动作。

Sub-game

子赛局的定义，可以很自然地从Game Tree中引申出来。

Definition of Sub-game: 一个game tree，从一个资讯结点出发，一路到game结束。这样的一个子树叫做子赛局。

如果知道树，那就很清楚。子赛局的概念就是离散数学中的子树。

Construct the strategic form from its extensive counterpart

有了extensive form，我们自然想到这个问题，如何将一个game tree转化成一个normal form的形式？

具体而言，要完成如下的几个步骤：

1. Define a pure strategy for player $i$ as a complete description of which action player $i$ will take (with probability one) at each of his information sets.
2. if two pure strategies of player $i$ always generate the same payoff for player $j, \forall j \in \mathcal{I}$, then they are said to be equivalent, we shall delete all the equivalent strategies till 1 remain.
3. Write in a form.

相当于，定义每个player的策略$\rightarrow$删除等价的策略只剩下一个$\rightarrow$写入表格中。

需要注意的是，在找等价策略时，要让除了$i$之外的其他人保持他们的策略不动（即固定$\sigma_{-i}$）。如果player $i$有不同的策略产生相同的payoff，则这些策略是等价的。

The Next Move: Solve the Problem!

Stackelberg game （斯塔克伯格博弈）

We want to apply the procedure of backward induction to solve the SPNE for the Stackelberg game.

问题定义：

规则是：

1. 厂1先做动作（称为市场上的leader）
2. 厂2看到厂1选择的$q_1$，自己选择$q_2$来对付$q_1$
3. 厂1和厂2生产的产品是同质的

我们来解这个问题。

Solution. 由题意，价格的表达式为：

\[P = 1 - q_1 - q_2\]

按照题目假设，厂商$1$首先选择一个产量$q_1$。依据backward induction，我们先考虑厂商$2$。厂$2$要选用一个$q_2$来对付$q_1$，应该有：

\[q_2^* = argmax(q_2 (1-q_1-q_2))\]

记

\[f = (1-q_1)q_2 - q_2^2 \Rightarrow f^{\prime} = (1-q_1) - 2q_2 \Rightarrow q_2^* = \frac {1- q_1} {2}\]

这样我们找到了厂$2$的产量$q_2$函数对应式。假设厂2选择了产量$q_2^*$（表示厂2在厂1采取$q_1$产量后的反应产量$q_2$）则这里看厂$1$，应有：

\[q_1^* = argmax(q_1(1-q_1 - q_2^*))\]

记

\[g = q_1(1-q_1 - q_2^*) \Rightarrow g^\prime = \frac {1} {2} (1 - 2q_1) \Rightarrow q_1^* = \frac {1} {2}\]

所以解得

\[q_1^* = \frac {1} {2}, q_2^* = \frac {1} {4}\]

但注意，问题到这里暂时还不算完。

如果厂1经过一番计算，知道厂2要采取$q_2 = \frac {1} {4}$的策略对付他，那厂1就会想要偷偷减产！

这时候，有：

\[payoff_1 = q_1(\frac {3} {4} - q_1) \Rightarrow q_1^* = \frac {3} {8}\]

如果是这样，厂2也不信任厂1，双方互相预判，就回到了经典的Cournot Game。均衡是$q_1 = q_2 = \frac {1} {3}$.

So how to do? Make a commitment! 厂1要让厂2知道一旦自己选择了$1/2$的产量，就永远不会改变了。这时候厂2才会心甘情愿选择$1/4$的产量，让这个赛局的利益最大化。

继续，注意到：

\[q_2^* = \frac {1- q_1} {2}\]

可以看出这是一个关于$q_1$的减函数。因此，经常有市场的leader故意增加产量，逼迫follower减产，从而获取额外利益。这也解释了为何均衡时的价格相较于Cournot Game略低。

Reference

This note is mainly derived from Chyi-mei Chen’s Game Theory with Applications to Marketing and Finance, I Course @ National Taiwan University. Thanks him for giving this kind of excellent lecture.