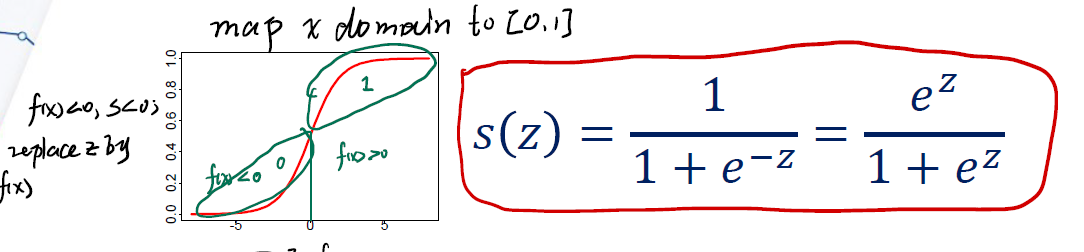DA06 Supervised Learning

DA06 :: Supervised Learning

In DA06, we shall talk about supervised learning methods.

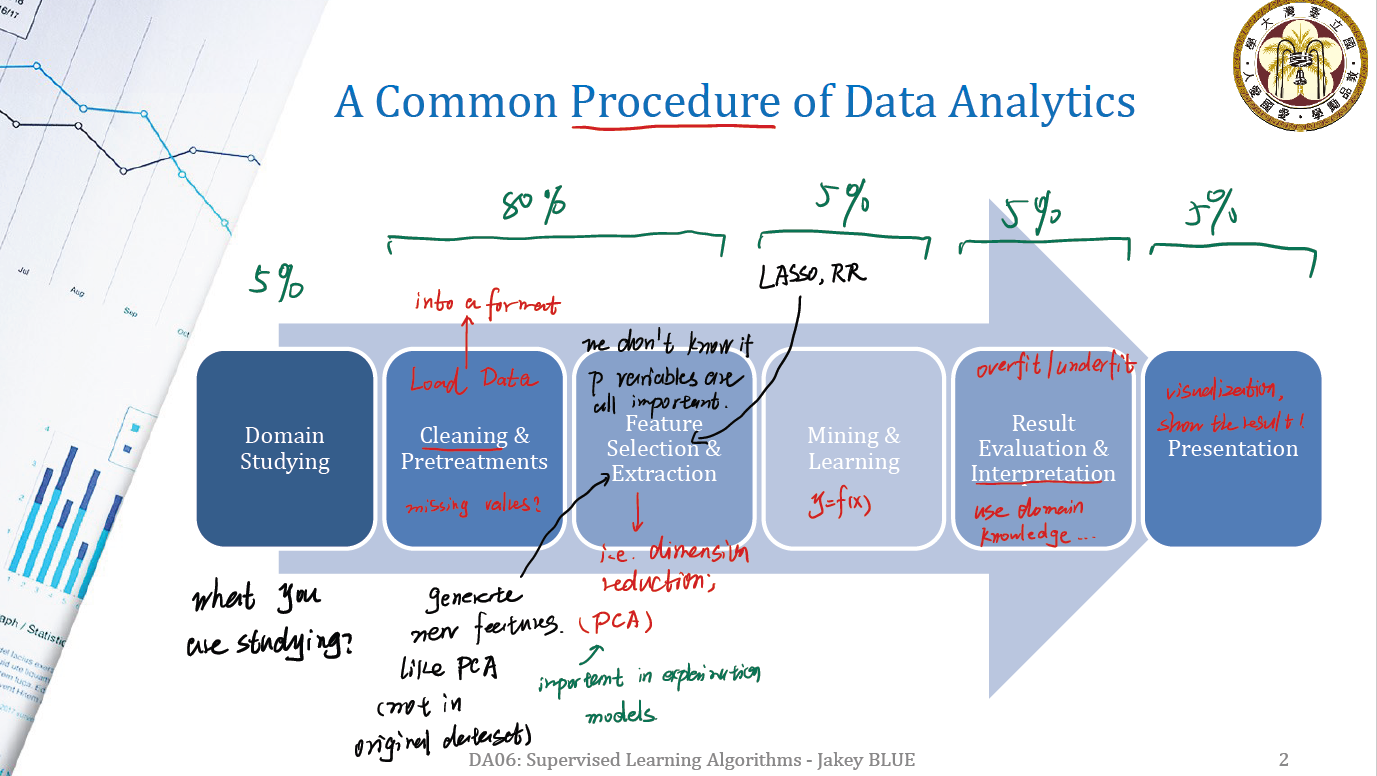
Common Procedure of Data Analytics

• Domain Studying: Consider what you are studying. May related to some domain knowledge.
• Cleaning & Pretreatments: This part we need to load data into some certain format, i.e. DataFrame
• Feature Selection & Extraction: This part is an important part. We do not know if $p$ variables are all important. So we may want to do some cut. Generally, this part include:
  • generate new features which are no tin original dataset. (like PCA)
  • dimension reduction (such as LASSO, RR)
• Mining and Learning: Construct the model, such as $y = f(x)$.
• Result Evaluation & Interpretation: This part we may use some domain knowledge, to translate statistics to description results. What’s more, we also need to consider overfit/underfit question.
• Presentation: Show our result.

What is supervised learning?

Supervised Indicates Additional Info other than original dataset $X$.

例如，我们有 dataset $X$ 。

\[X = \begin{gathered} \begin{bmatrix} x_{11} & x_{12} & ... & x_{1p} \\ x_{21} & x_{22} & ... & x_{2p} \\ \vdots \\ x_{n1} & x_{x2} & ... & x_{np} \end{bmatrix} \end{gathered}\]

$X$ 这个数据集本身有 $n$ 行， $p$ 列。但是我们除了这个数据集外，可能还有与之对应的 response matrix $Y$ 。

\[Y = \begin{gathered} \begin{bmatrix} y_{11} & y_{12} & ... & y_{1q} \\ y_{21} & y_{22} & ... & y_{2q} \\ \vdots \\ y_{n1} & y_{x2} & ... & y_{nq} \end{bmatrix} \end{gathered}\]

因此，我们就达成了 supervised learning 的必要条件：Additional Information 。

Decide Training Scheme before Applying Algorithms

在使用 supervised learning 算法之前，首先要考虑的是如何训练的问题。

我们通常将 dataset 分成 training set 和 testing set 。

• training set ：用来找出模型的参数，从而构建模型。

• testing set ：用来检验构建的模型是否好。

此外有的时候，可能还需要对数据集进行打乱抽取。要注意的是，如果数据集是像 mpg 这样的，没有时间上先后顺序的，打乱抽取是OK的。但是如果数据集是 time series ，则肯定不能打乱数据的顺序。因为这时候数据的顺序很重要。打乱了就破坏了 information 。

Training and Testing

3 ways to Train the classification model

在训练的过程中，我们有三种常用的处理数据集将其分成training set 和 testing set 的方法。

Hold-out

Hold-out 方法是最简单粗暴的方法。在一开始就直接划定一个 training set 和 testing set 之间的比例。例如，直接划定 $1/3$ 的数据用来做 testing ；$2/3$ 的数据用来做 training 。

k-Fold Cross Validation

k-fold 是现在用的一种流行方法。

• 首先，将数据集分成k份，每次用一份（称为 one-fold ）做 testing 。
• 重复 $k$ 次。观察每一次 testing 的模型的结果是否有显著差异。
• 经验上取 $k = 10$ 。

这样做其实是考虑：”Are they always performing similarily in terms of traning and testing?”

如果模型在这些 fold 上都表现的差不多，则说明模型处理这一些数据的能力还可以，不会因为数据的变化而变化太多。但如果模型在某些 fold 上表现的很差，说明如果选择不同的数据，模型的处理能力不好，模型可能不太适合分析这个 data set 。

Bootstrap

Bootstrap 是一种”创造新数据”的处理方法，很适合在小规模数据集上使用。

• 首先，在样本中随机进行有放回地抽取。（ Random sampling uniformly with replacement ）
• 然后，对抽取出来的这一个 data set 做 training 。
• 这样重复步骤。

Example of Bootstrap method

假如我们有一个很极端的数据集。总共有 100000 笔 data 。其中，正常的数据有 99990 个，异常的数据有 10 个。

如果采用k-fold进行，我们很难进行训练。分成 10 个 fold ，每个 fold 中只有 1 个异常数据，模型很难学到异常数据到底哪里不对。

但如果我们使用 Bootstrap 方法，就可以一定程度上做到比 k-fold 方法好。

我们处理的方法为：

1. 随机在数据集中抽 1000 个点（有放回，这样就增加了抽到 abnormal 数据的可能性）
2. 在抽取后，进行 training 。

Hint: 也可以更改 pick-scheme 。例如，我们设定 1000 笔抽取出来的资料，必须要有 50 笔异常。这种处理称为 down-sampling 或 up-sampling 。

这样处理下来，N 个 observation ，N次都没被选中的概率应该是：

\(\text{P(a sample is never chose)} = (1 - \frac {1} {N})^N\) 当 $N \rightarrow \infin$ 时，这个概率的极限为 $e^{-1} = 0.368$ 。

Evaluate performance of our model: Confusion Matrix

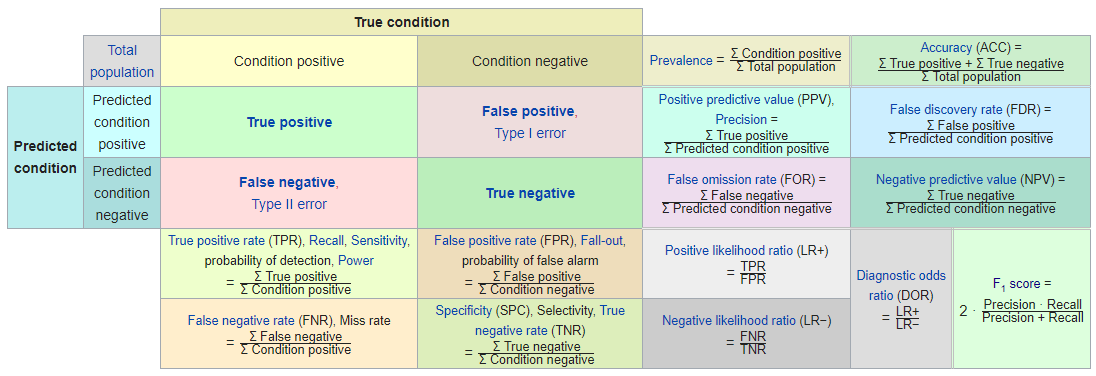
实务上，常用 Confusion Matrix 进行模型的 evaluate 。

在 Confusion Matrix 中；

• True Positive (TP): 这是预测为 Positive ，且结果为 True 的情况，是 good result of model 。
• False Positive (FP): 预测是 Positive ，但结果是 False 的情况，称为假阳性。
• False Negative (FN): 预测是 Negative ，但结果是 True 的情况，称为假阴性。
• True Negative (TN): 预测是 Negative ，实际也是 False 的情况，是 Good Result 。

我们经常用的度量方法有 accuracy （准确率）、sensitivity（敏感性）、specificity 和 precision 。下面分别介绍这四个度量方法的计算，以及它们代表着什么。

Accuracy

计算公式为：

\[\text{accuracy} = \frac {TP + TN} {TP + FP + FN + TN}\]

可以发现 accuracy 主要针对的是预测与事实相一致的情况。判断准确率。

sensitivity

计算公式为：

\[\text{sensitivity} = \frac {TP} {TP + FN}\]

sensitivity 主要研究的是为 True 的那些观测值。它想知道，在本身就是正确的（True）的那些observation中，模型正确地分辨出了多少？

specificity

计算公式为：

\[\text{specificity} = \frac {TN} {FP + TN}\]

specificity主要研究的是为False的观测值。它想知道的是，本身是False的observation中，模型正确地找出了多少错误？

precision

计算公式为：

\(\text{precision} = \frac {TP} {TP + FP}\) precision研究的是，在模型预测 observation 的对应类别为错误的情况下，有多少是真的错了的。

当然还有更多的说法……

F1-score

F1 score主要是检验测试的结果的，计算表达式为：

\[\text{F1-score} = \frac {\text{precision} \times \text{recall}} {\text{precision} + \text{recall}}\]

我们期望这个值越高越好。

Receiver Operating Characteristic (ROC) Curve

ROC Curve 是一个很有用的工具，能够帮助我们在一定程度上可视化 TPR (True Positive Rate) 和 FPR (False Positive Rate) 之间的关系，从而告诉我们如果模型给出 Positive 的预测，有多少是正确的。加上 FPR ，可以很好地判断模型犯Type-I error 的错误。（更加关心Type-I error，即”无罪判有罪”）

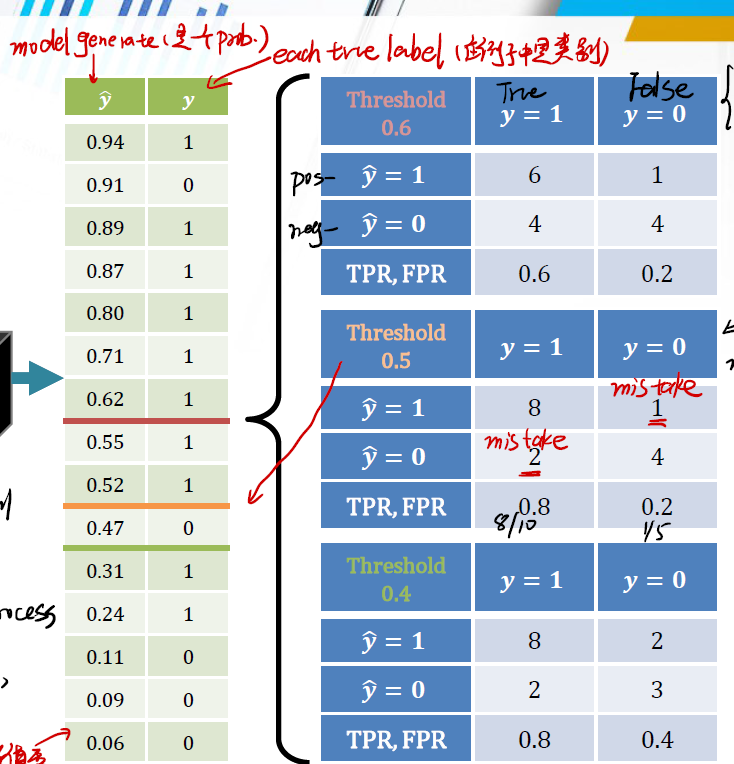
假设我们使用了三种不同的模型，每个模型在经过计算之后，设置一个 Threshold 。如果超过这个 Threshold ，则判断为 true ，没超过判断为 false 。我们的数据和计算如下：

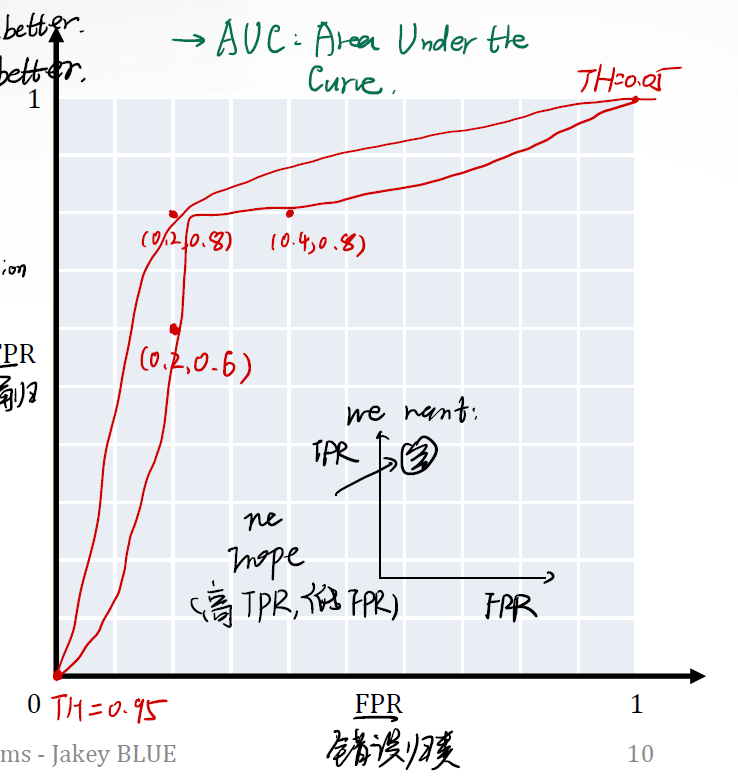
可以看到有三个不同的模型，分别取 threshold 为0.6，0.5，0.4。现在针对这三个，我们分别求出对应的 TPR 和 FPR。并以 FPR为x轴，TPR为y轴绘制ROC曲线：

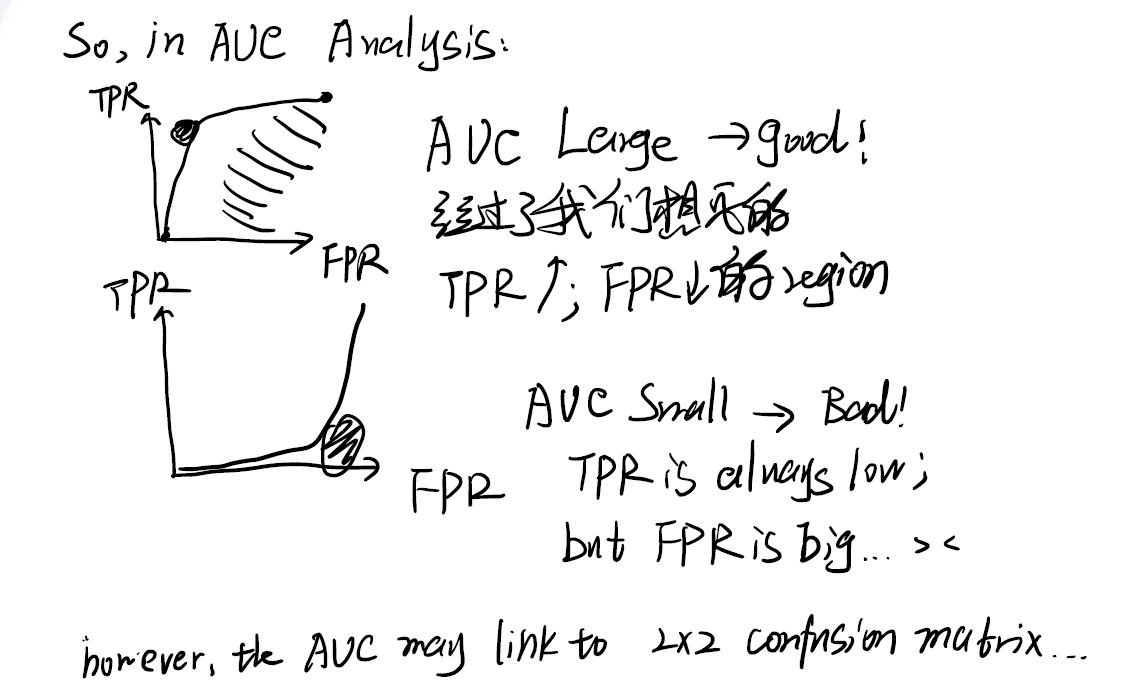
我们期望点都分布在左上角。左上角代表着低FPR，高TPR。

与ROC曲线对应的是AUC（Area Under the Curve）。它代表着ROC曲线下的面积。

• 如果面积大，意味着曲线向左上角弯，曲线经过了我们想要的区域（左上角，小FPR大TPR），模型表现不错。

• 如果面积小，意味着曲线向右下角，曲线没经过了我们想要的区域（左上角，小FPR大TPR），模型表现差。

不过，AUC似乎只适用于 $2 \times 2$ 的matrix，如果是 $3 \times 3$ 甚至更多呢？

可能，如果有三个类别，我们要做三个matrix，每个matrix都代表模型是否识别出了某一类。这样变成 $2 \times 2$ 的matrix，就可以进行ROC分析了。

Common Classification Methods

接下来我们来看一些常用的分类方法。

Logistic Regression

Logistic Regression 是一个很基础的分类方法。我们先来介绍它是怎么做的。

Introduction to Logistic Regression

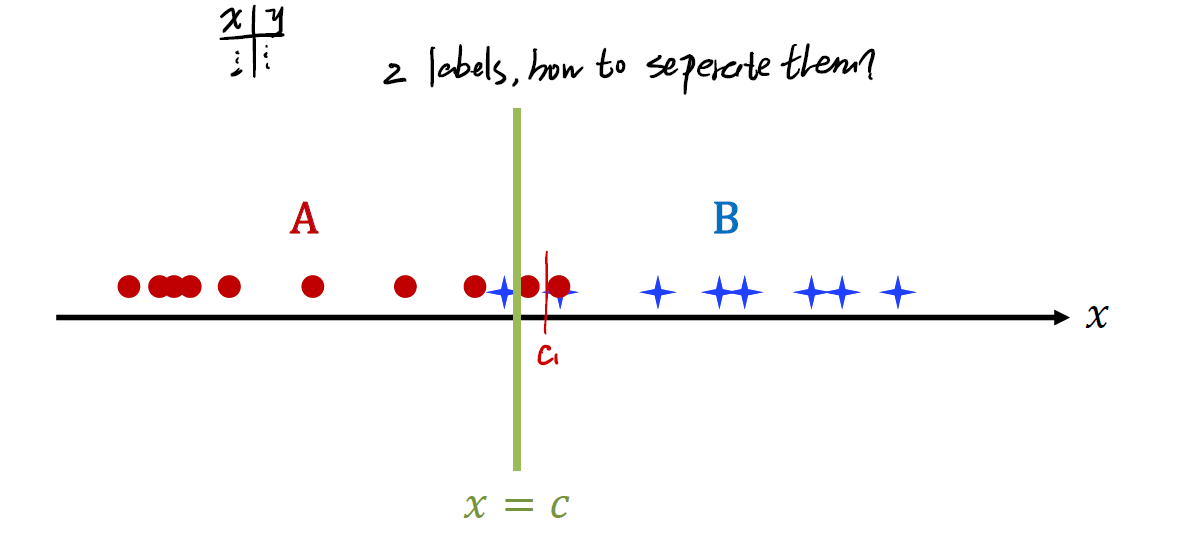
给定一个一维的 data，想要对其进行分类：

第一个方法是Linear Regression。

直接用一条直线来做拟合，随后插入一个cut-point。point左侧的是一类，右侧的是另一类。当然，这种情况肯定不是很准确。

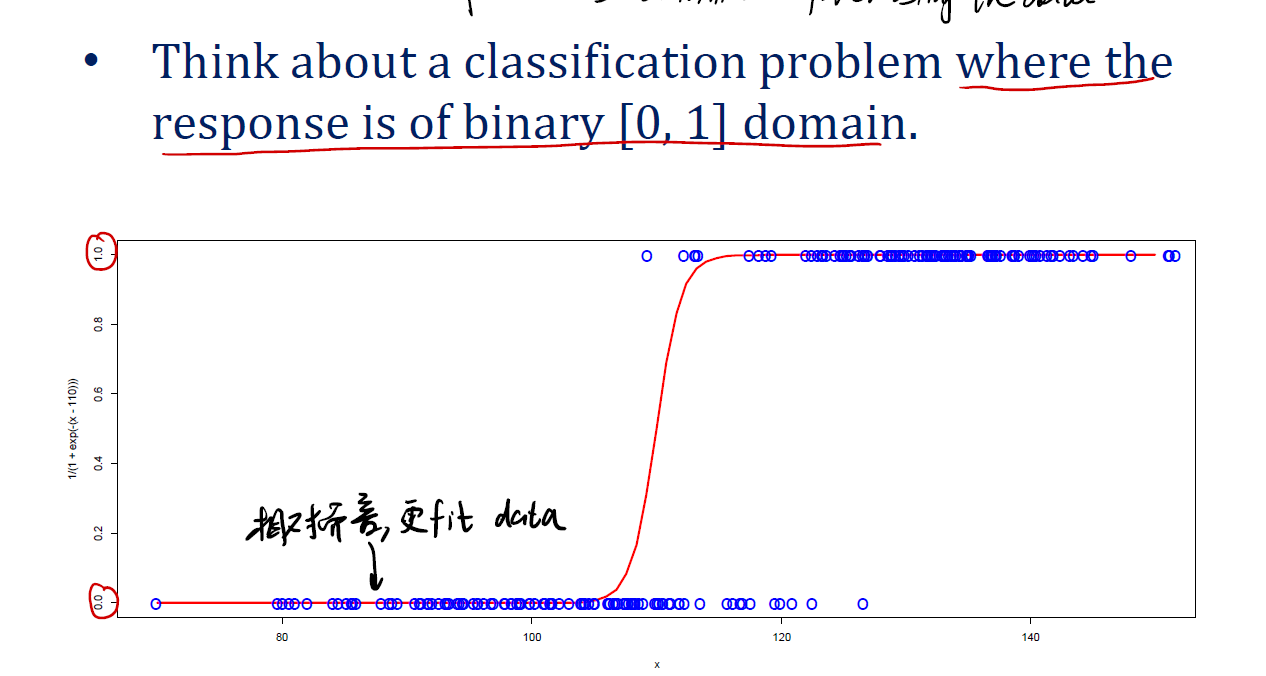
如果能换成一根曲线呢？

Change to curve

Logistic function (Sigmoid function)

logistic function 的表达式为：

\[s(z) = \frac {1} {1 + e^{-z}} = \frac {e^z} {1 + e^z}\]

该函数可以将$\mathbb{R}$映射到$[0, 1]$。其中，若 $x < 0$ ，则 $s(z) < 0.5$ ； $x > 0$，$s(z) > 0.5$ 。

如果用0.5作为判断 $y$ 类别的threshold，则可以将模型写为：

\[y = \text{sigmoid}(f(x)) = \left\{ \begin{array}{**lr**} 0,& f(x) < 0 \\ 1, & f(x) \ge 0 \end{array} \right.\]

这样就可以将 $x$ 分为 ${ 0, 1 }$ 两个类别。

同样可以写出 $x$ 所属类别的概率：

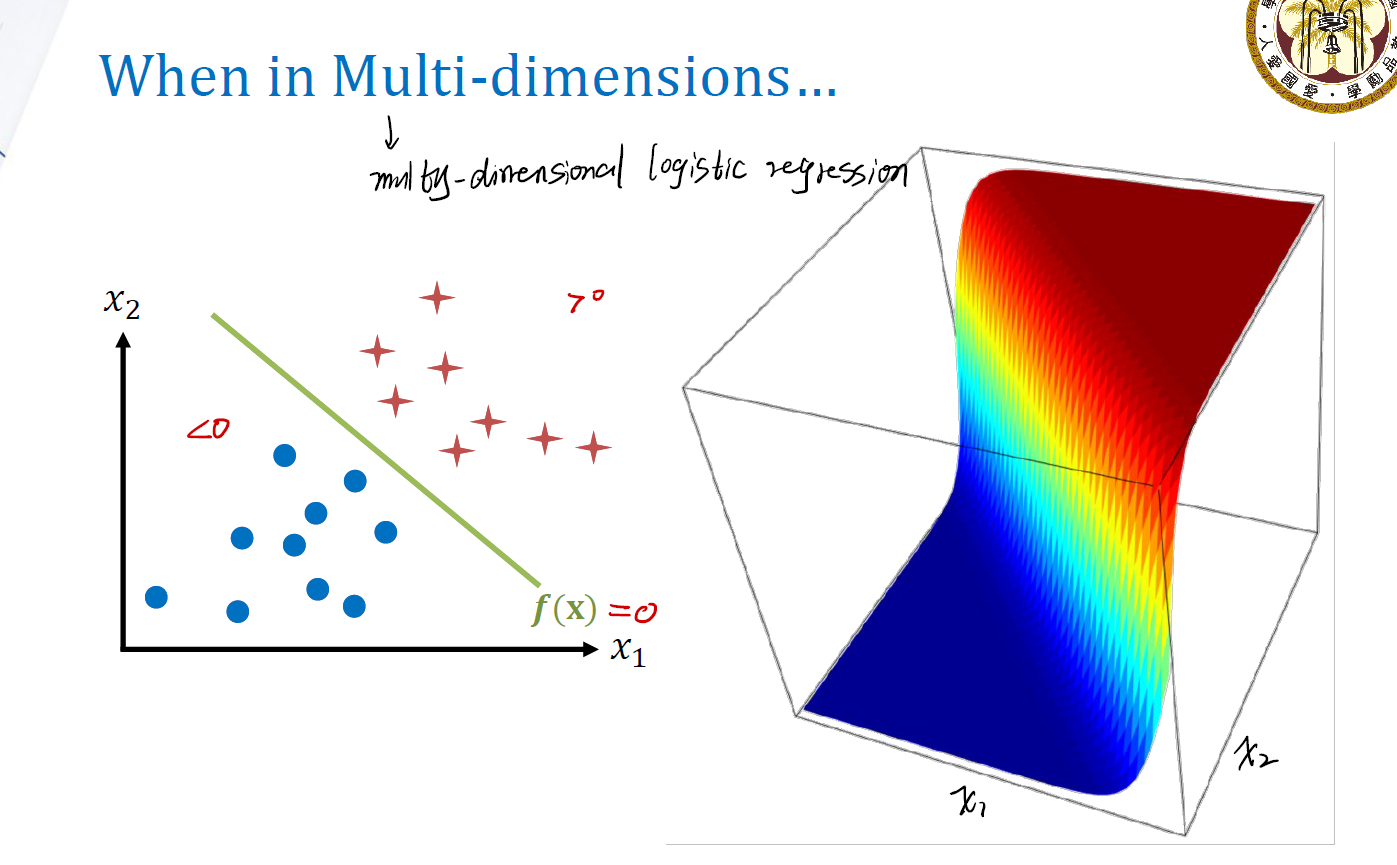
\[p(y = 1 | x) = \frac {1} {1 + e^{-f(x)}} = \frac {e^{f(x)}} {1 + e^{f(x)}}\]

假如有多个 $x$ ，例如 $\mathcal{x} = (x_1, x_2, … x_n)$ ，那此时，$f(x)$ 将成为 $x_1$ 与 $x_2$ 的combination。即：

\[f(x) = x\beta\]

在这时，我们所做的learning就很简单：找到合适的$\beta$，使得能最好地结合$x_1$与$x_2$即可。此时： \(p(y = 1 | x) = \frac {1} {1 + e^{-f(x)}} = \frac {e^{f(x)}} {1 + e^{f(x)}} = \frac {e^{x\beta}} {1 + e^{x\beta}}\)

How to find $\beta$ ?

上面已经提到要找到合适的 $\beta$ 来做combination。现在来看怎么做combine。

首先可以将$x$属于第1类的概率写成：

\[p_x = \frac {1} {1 + e^{-x\beta}}\]

两边同取log函数：

\[\log (\frac {p(y = 1 | x)} {1 - p(y = 1 | x)}) = x\beta\]

上面log函数内部的式子其实是 $\text{success rate} / \text{failure rate}$。现在想估计 $\beta$，就要找log这一个函数怎么计算，从而做regression。

但真的能做regression吗？

考虑到我们有的数据，只有两个部分：

1. 标注的数据$x$；
2. 每个$x$对应的类别（1或者0）。

条件概率的计算是：

\[p(A|B) = \frac {p(A\cap B)} {P(B)}\]

在这里，计算条件概率：

\[p(y = 1 | x) = \frac {p(y = 1, x)} {p(x)}\]

但是我们并不知道$p(x)$是多少，因为我们根本没法采集到总体的数据。因此log无法计算出来，MSE也很难使用。

Maximum Likelihood Helps…

所以，只有一个选择：极大似然估计。

现在开始做极大似然估计。对每一个$x_i$，都有：

\[p_i = p(y_i = 1 | x_i)\]

写出似然函数是：

\[\mathcal{L}(\beta) = \prod_{i = 1}^{n} p_i^{y_i}(1 - p_i)^{(1 - y_i)}\]

注意这里是二元分类，所以似然函数里用的是bernulli distribution的几率分布函数。

接下来就是常规，两边同取log：

\[-\log (\mathcal{L}(\beta)) = -\sum_{i = 1}^n(y_i\log (\frac {p_i} {1 - p_i}) + \log (1 - p_i))\]

然后分离$\beta$出来。