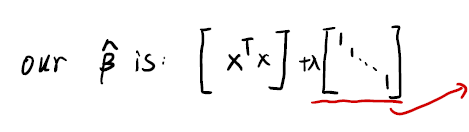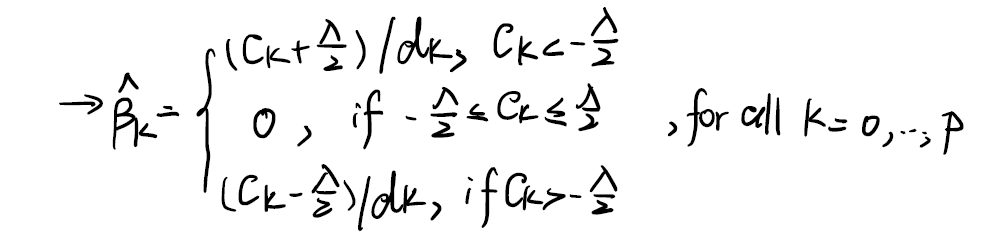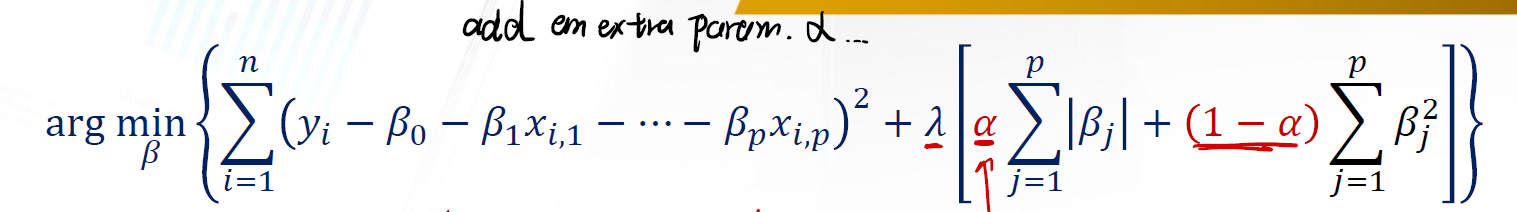DA04 Dimension Reduction, Part I

DA04 Dimension Reduction :: Part I Note

This is DA04 part I note. Include some detail of feature selection and penalized regression.

Why do we need to reduce the dimension?

This is an interesting and basic question. Why reduce the dimension? Let’s see two kind of dataset.

A flatten dataset

首先来看这样的一个所谓“扁平”的数据集。我们有$X_{n \times p}$，其中$p » n$。这表示我们有$p$个回归变量，总共有$n$笔资料。

这时候出现了一个问题，资料的数目远远比回归变量的数目小。在 DA02 的几何意义诠释中，我们提到的情况是$n » p$。在那时，我们的目标是用低维度的信息来尝试逼近高维度的信息。在这里我们又该如何做呢？

$\rightarrow$ 一种想法是，我们可以使用 stepwise regression 来逐渐添加变量。否则的话，我们的计算过程将变得十分漫长。

A normal dataset

与扁平数据集对应的是正常的数据集。即$n » p$。这时候比较好处理。

在$p » n$的情况下，我们经常出现所谓的 维度灾难¹ 问题。我们该使用什么方法来解决这个问题呢？

Feature Selection or Extraction

维度灾难意味着我们使用了太多的$x_i$，即回归变量。一个很直觉的想法是，我们干脆挑选一批具有代表性的回归变量$x_i$出来不就好了？这就是所谓的 feature selection。

所谓的 feature ，就是一些重要的回归变量$x_i$。

常用的方法大致可以分为三类。分别是所谓的 Supervised method ，所谓的 unsupervised method 和所谓的 non-linear method 。其中：

• Supervised method 需要我们同时有 $x$ 和 $y$ 值。常用的有：
  • Subset Regression
  • Penealized Regression (will add little constraint on top of the regression)
    • Least Absolute Shrinkage & Selection Operator (Lasso Regression)
    • Ridge Regression (RR)
    • Elastic Net
  • Partial Least Squares Regression (A powerful regression method, it will be used in multiple regression case, and this method considers the cov. between $x$ and $y$ )
• Unsupervised method 我们并不要求有 $y$ 值。常用的有：
  • Principal Component Analysis (PCA)
  • Factor Analysis (FA)
• non-linear method 常用的有：
  • Independent Component Analysis (ICA)
  • Locality Preserving Projections (LPP)
  • t-distributed Stochastic Neighbor Embedding (tSNE)

我们将分别介绍。在 part 1 中，我们主要介绍 Supervised method 。

Subset Regression

在 Subset Regression 中，我们希望通过逐个对比不同模型的方法，找到一个最合适的模型，从而筛选变量。

以5个回归变量（ regressors ）的模型为例。我们可以通过增加/减少变量的方法来构建不同的 regression model 。

$1^\prime$ 构建 simple regression model ，如 $y = \beta_0 + \beta_1x_1$的形式，总共会有 $C_5^1$ 种 simple regression 模型；

$2^\prime$ 构建复杂的模型，分别选 2， 3， 4， 5 个 regressors ，可以分别得到 $C_5^2$ , $C_5^3$, $C_5^4$ , $C_5^5$ 种模型。

我们就在这31个模型中选择。可以利用我们前面提到的 R-Square , Adjusted R-Square , AIC , BIC 来筛选。

不过要注意的是，这只是一个仅含有 linear term 的模型。我们没法筛选具有交叉项（如 $x_1x_2$ ）的模型。

How to identify key regressors?

那完成了所谓的模型筛选，我们又如何界定什么是关键的回归变量呢？

直觉的方法是，比较 $\beta_i$ 的大小，或者比较 $\beta_i$ 对应的 p-value 的大小。但这真的合理吗？

If … Comparing $\beta_i$ ?

$\text{large } \beta_1 , \text{small } \beta_2 \longrightarrow \text{we shall choose } \beta_1 \text{ rather than } \beta_2 $ (Is this right?)

如果比较 $\beta_i$ ，有一个致命的问题。

仍然以 DA02 中的 mpg 回归问题为例。我们能发现，回归系数的值很容易受到回归变量量纲的影响。一个 $\beta$ 值很低，不一定代表对应的 regressor 不重要，也可能是这个 regressor 的量纲太大了，导致必须要一个小的 $\beta$ 来“配平”。

如果想要用 $\beta$ 的值来筛选 regressor ，那至少要做一次针对 $x$ 的标准化。

If … Comparing the p-value of $\beta_i$

是否有所谓的 “small p-value, more significant” 呢？答案依旧是 No 。

注意我们的 p-value ，仅仅是用来进行假设检验的！极小的 p-value 只能说明 $\beta$ 值与 0 大相径庭，而不能说明 $\beta$ 值背后的 regressor 在我们的模型中很重要。

Here are OK ways…

有两种方法来筛选。

$1^\prime$ 先对 variables 进行标准化，然后做回归。这样统一了量纲 ( same scale )，$\beta$ 的值就变得有意义了。可以说明哪些 regressor 很重要。

标准化的公式为：

\[z_i = \frac {x_i - \bar{x_i}} {S_i}\]

然后构建新的回归模型

\[y = \beta_0 + \beta_1z_1 + ... + \beta_pz_p\]

这时候的 $\beta_i$ 可以表示，$z_i$ 变动一个 unit ，$y$ 会变动多少。这就是 $z$ 对 $y$ 的影响！可以进行一定程度的变量筛选。

$2^\prime$ 当使用 stepwise 方法移除变量时，利用 adjusted R square 进行筛选。

Penalized (Regularized, Shrinkage) Regression

下面我们来介绍所谓的 Penalized Regression 方法。这种方法将用选定的关键变量来构建回归模型。分别介绍 Least Absolute Shrinkage & Selection Operator , Ridge Regression 与 Elastic Net 。

Least Absolute Shrinkage & Selection Operator ( Lasso )

Lasso 是一种通过增加 Constraints ，以期望限制原本 LSE 模型的规模，从而控制模型参数 $\beta$ 个数的一种回归方法。

在最小二乘回归中，我们期望求解的的等式是：

\[\arg \min_\beta \sum^n_{i = 1} (y_i - \beta_0 - \beta_ix_{i, 1} - ... - \beta_px_{i, p})^2\]

在最小二乘回归的基础上，我们期望加上一些限制条件，从而来限制 $\beta$ 的规模。我们添加的限制条件为：

subject to:

\[\sum^p_{j = 1} |\beta_j| \leq t\]

where $t$ is a tuning factor.

这里加入的限制条件如上。我们称这个限制条件为所谓的 L1-norm constraint 。

我们也可以利用凸优化的相关知识，将上面两式合并为一个，即：

\[\arg \min_\beta \sum^n_{i = 1} [(y_i - \beta_0 - \beta_ix_{i, 1} - ... - \beta_px_{i, p})^2 + \lambda \sum^p_{j = 1} |\beta_j|] -\lambda t\]

这样我们后续便可以对这个式子进行 minimize 操作。我们将 $\lambda$ 称为 lagrange multiplier 。

In Lasso, we want to Kill the coefficient beta. We hope our constraint shrink those insignificant or small $\beta$ , and force them to be 0.

Ridge Regression (RR)

在所谓的 Ridge Regression 中，我们更换了 constraint ，但是整体的目标和架构与 Lasso 没什么出入。

\[\arg \min_\beta \sum^n_{i = 1} (y_i - \beta_0 - \beta_ix_{i, 1} - ... - \beta_px_{i, p})^2\]

subject to:

\[\sum^p_{j = 1} \beta_j^2 \leq t\]

where $t$ is a tuning factor .

The equivalent expression is:

\[\arg \min_\beta \sum^n_{i = 1} [(y_i - \beta_0 - \beta_ix_{i, 1} - ... - \beta_px_{i, p})^2 + \lambda \sum^p_{j = 1} \beta_j^2] -\lambda t\]

where $\lambda$ is also a Lagurange Multiplier. We want to estimate $\beta_0,\beta_1, \dots, \beta_p$.

Mathematic behind RR

现在我们来看 RR 背后的一些数学原理。实际上 RR 和正常的回归很想，只不过双方的限制不同。

在 RR 中，我们期望进行优化的函数表达式是：

\[\mathcal{L} = \lvert \lvert y - x\beta \rvert \rvert + \lambda \lvert \lvert \beta \rvert \rvert = (y - X\beta)^T(y - X\beta) + \lambda \beta^T \beta\]

其中， $ \lvert \lvert y - x\beta \rvert \rvert$ 是我们的最小二乘，而 $\lambda \lvert \lvert \beta \rvert \rvert$ 是所谓的 L2-norm 。我们对 $\mathcal{L}$ 求取偏微分：

\[\frac {\partial \mathcal{L}} {\partial \beta} = 2X^TX\beta - 2X^Ty + 2\lambda \beta = 0\]

解得：

\[\hat{\beta} = (X^TX + \lambda I)^{-1}X^Ty\]

这就是我们在 Ridge Regression 的限制下求得的 $\hat{\beta}$ 的估计式。

那现在，所谓的 ridge 在什么地方？

$\longrightarrow$ ridge is coming from $\lambda I$ part.

我们的 $\hat{\beta}$ 是：

注意到右边的是一个 diagonal matrix。我们将把 $\lambda$ 值加在矩阵 $X^TX$ 的对角线上，这就是所谓的 ridge 的来源。

Mathematic behind Lasso: Not an easy case

然而在 Lasso 中，是一个比较麻烦的事情。因为我们采用了带有绝对值的 L1-norm。这让问题变得复杂了一些。

在 Lasso 中，我们必须假设 $X^TX = I$ 成立，才会有 closed form solution。然而在实际过程中，这个假设基本上是很难达成的。我们必须用机器学习的方法来解决这个问题

现在，我们来对 Lasso 的最优化过程进行处理。我们总共有 $n$ 笔资料， $p$ 个回归变量。

\[f = \sum_{i = 1}^n [y_i - \sum_j^p x_{ij} \beta_j]^2 + \lambda \sum_j^p |\beta_j|\]

现在对 $\beta_k$ 求偏微分：

\[\frac {\partial f} {\partial \beta_k} = -2\sum_{i = 1}^n [x_{ik} (y_i - \sum_j^p x_{ij} \beta_j)] + \text {?}\]

这里用一个小 trick ，将 $\beta_k$ 分离出来：

\[\begin{align*} \frac {\partial f} {\partial \beta_k} & = -2\sum_{i = 1}^n [x_{ik}y_i - (x_{ik} \sum^p_{j \neq k} x_{ij} \beta_j) + x_{ij}^2 \beta_k] + \lambda \\ & = -2\sum_{i = 1}^n [x_{ik} (y_i - \sum_{j \neq k}^p x_{ij} \beta_j)] + 2\sum_{i = 1}^n x_{ik^2} \beta_k \end{align*}\]

让左边的为 $C_k$ ，右边的为 $D_k$ 。上式变成：

\[= -2C_k + 2D_k\beta_k \\\]

现在处理偏微分时候我们留下的 ? 项：我们有：

\[\frac {\partial \lambda \sum |\beta_j| } {\partial \beta_k} = \left\{ \begin{matrix} \begin{align} & -\lambda, & \beta_k < 0 \\ & [-\lambda, \lambda], & \beta_k = 0 \\ & \lambda , & \beta_k > 0 \\ \end{align} \end{matrix} \right.\]

我们现在可以合并前面的结果了。我们有：

\[\frac {\partial f} {\partial \beta_k} = \left\{ \begin{matrix} \begin{align} & -2C_k + 2D_k\beta_k -\lambda, & \beta_k < 0 \\ & -2C_k + 0 + [-\lambda, \lambda], & \beta_k = 0 \\ & -2C_k +2D_k\beta_k + \lambda , & \beta_k > 0 \\ \end{align} \end{matrix} \right.\]

现在令其为0，我们便可以得到 $\beta_k$ 的估计值 $\hat{\beta_k}$ 。并将关于 $\beta_k$ 的条件转化为关于 $C_k$ 的条件：

那这样我们就得到一个计算 $\hat{\beta_k}$ 的方法。我们可以采用诸如梯度下降的方法来逼近真实值。

How do I know when do I use these 3 values? We need to check the condition.

1. $\lambda$ is a given value, we can randomly assign a $\beta$. and $C_k$ can be calculated.
2. After many rounds, we can get a stable $\beta_k$.

$\longrightarrow$ So how to assign $\lambda$ ? This is just what you want. :-)

Geometrical Meaning of LASSO and Ridge Regression

现在我们来看 Lasso 和 Ridge Regression 的几何意义。

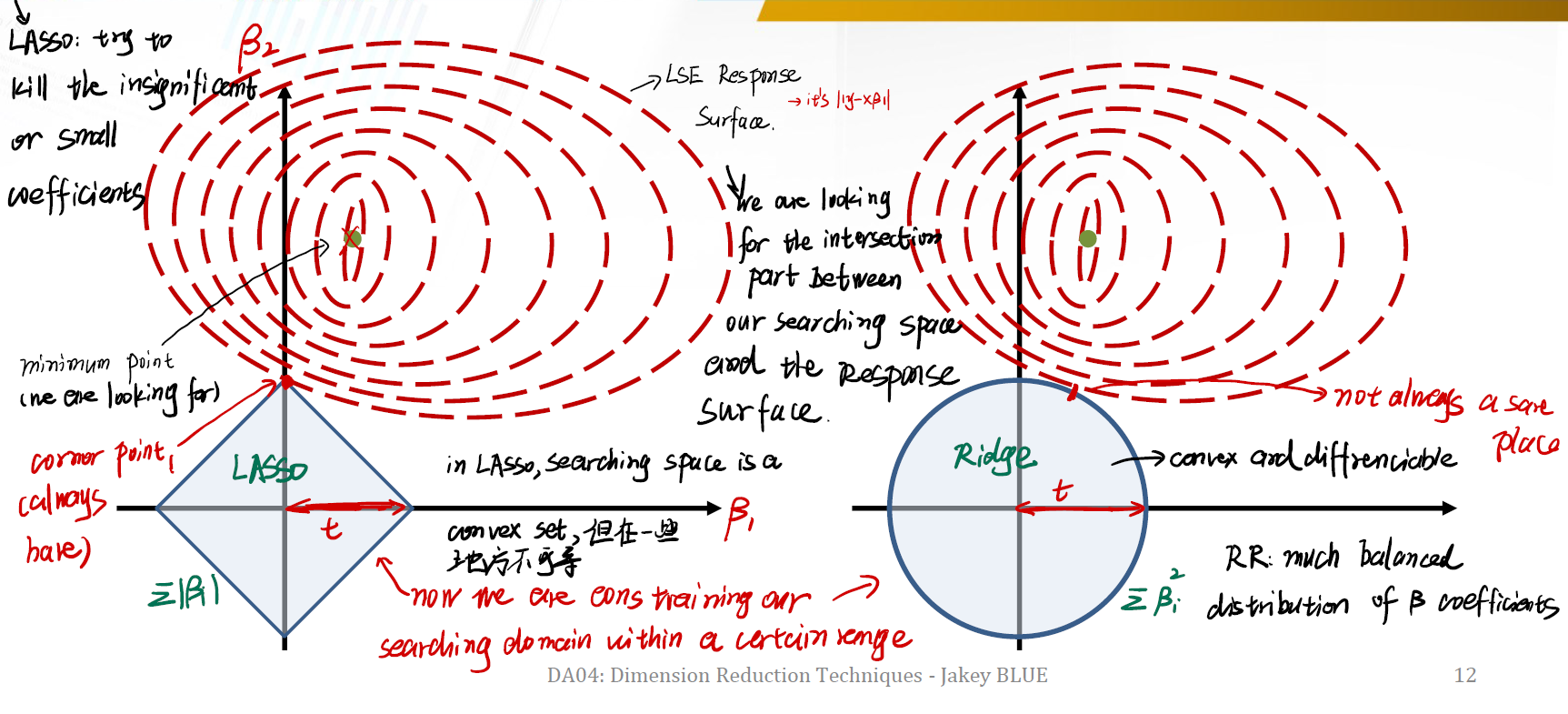
左边是 Lasso 的几何图像，右边是 Ridge 的几何图像。

首先要牢记，Lasso 试图去掉那些不显著或者很小的 $\beta$ 值，而 RR 并不试图这么做。

红色虚线是最小二乘估计的 Response Surface 。我们当然期望找到所谓的 minimum point ，我们可以构建特别复杂的模型来做到。但通过加入 constraint ，我们限制了我们的 searching space 的规模。我们希望在这个限制后的 searching space 中，寻找到一个部分。这个部分是 searching space 与 response surface 的最近的交集。从而得到一个恰当的估计值。

对于 Lasso 来说：

• 限制条件 $t$ 决定了方形的 searching space 的宽度。
• 在 Lasso 中，边界是笔直的。这意味着我们想要找的解肯定在边界的 corner point 上，即左图的红点。并且这个 corner point 总是存在。
• 这个点就是与 response surface 的唯一交集，也是一个恰当的估计值。

在 Ridge 中：

• 同样的，限制条件 $t$ 决定了 searching space 的宽度。不过 RR 中 searching space 是一个圆形。
• 意味着我们想要找的解肯定在边界上，不过这里是一段边界，而非某个点。
• 这个边界就是我们的估计值。我们认为 RR 是一个 much balanced distribution of coefficients。

LASSO vs. Ridge Regression (RR)

$\lambda$ 的影响：

• $\lambda$ 大 $\rightarrow$ 会尝试让我们的回归系数 $\beta$ 尽可能地趋近于0。
• $\lambda$ 为0 $\rightarrow$ 就是正常的线性回归模型。

还有一个是对抗 collinearity 的影响：

在 collinearity 出现时，我们有 $(X^T X)^{-1}$ 不存在。然而，由于我们增加了一个 $\lambda$ ，总是会有 $(X^T X + \lambda I)^{-1}$ 存在。

因此，Lasso 和 RR都可以避免多重共线性带来的影响。

不同的是，Lasso 试图去 kill 掉某个回归变量，而 RR 试图找到一个平衡的方法，去对出现 collinearity 的变量进行一些均等的权重分布，使其都尽可能地小。

Elastic Net

有的时候，我们既希望能 kill 掉一些变量，又能很好地控制一些变量趋近于0。这时候自然有一个问题，如何 Combine Lasso 和 RR ？这就是 Elastic Net 的来源。

Elastic Net 加入了一个所谓的 Smoothing Factor $\alpha$ 。它将控制利用 Lasso 和 Ridge Regression 的比例。准确的说， $\alpha$ 衡量了在 L1-Norm 和 L2-Norm 的 penalty 。

• $\alpha = 1 \Longrightarrow$ Lasso Regression
• $\alpha = 0 \Longrightarrow$ Ridge Regression
• $\alpha \in (0, 1) \Longrightarrow$ Elastic Net

How Do We Fit the Penalized Regression?

Step #1: Choose and Fix $\lambda$

$\lambda$ 确定了限制的范围。一个很好的做法是用最小二乘估计来求初始的 $\lambda$ 。

Step #2: Choose $\alpha$

第二步是确定使用什么样的 $\alpha$ ，从而决定是用 Lasso，RR 还是 Elastic Net 。

• 使用 Lasso - 需要利用诸如梯度下降的方法来得到 $\beta_i$ 。在梯度下降的时候还要注意 $\beta_i$ 的符号问题。
• 使用 Ridge Regression - 有 closed form solution 。只需要解 $X^TX$ 即可。
• 使用 Elastic Net - 需要利用类似 Lasso 的方法来解决。

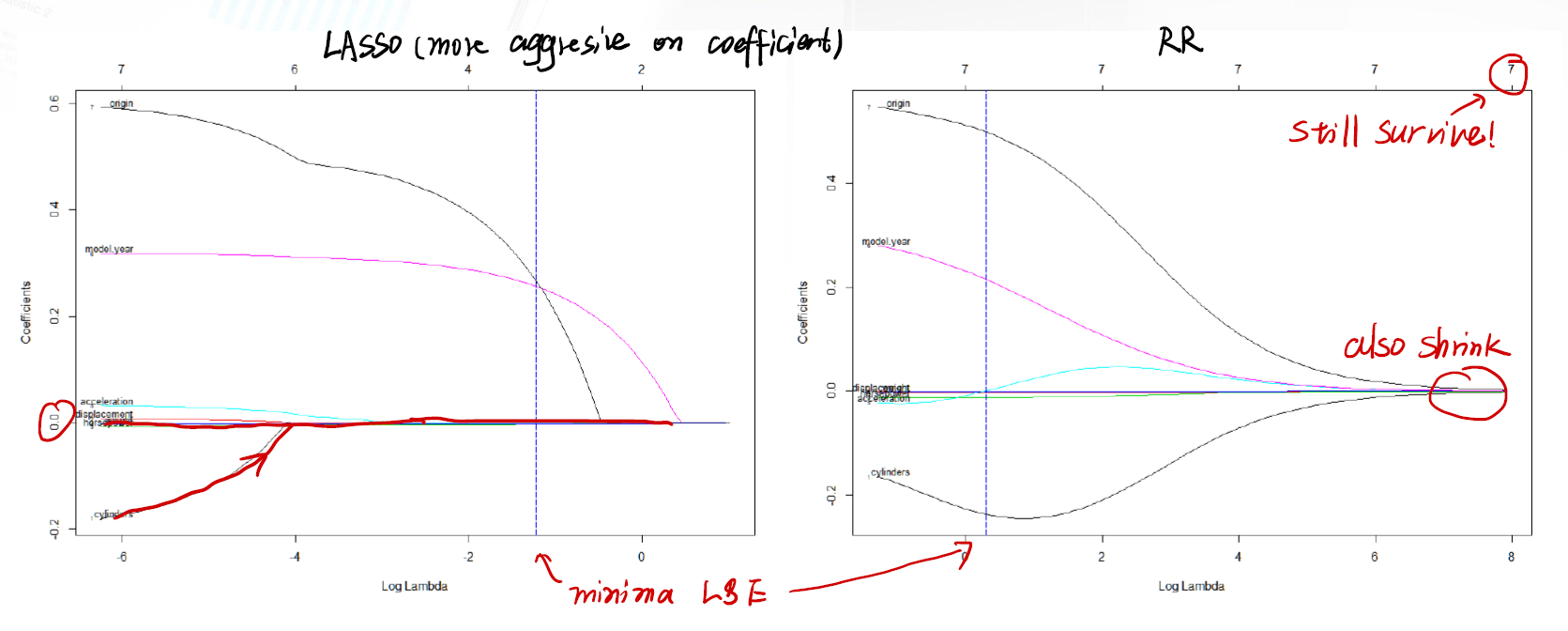
左边是 Lasso 的参数变化图。可以发现 Lasso 的参数归零非常快。右边是 RR 的参数变化图，可以发现即使 $\lambda$ 很大，参数仍然不会完全归零。

An Extra Question: Should we Normalize the Data?

We still need to normalize the data.

我们前面已经提过说，Lasso 和 RR 这一系列的回归方法，都只关注 coefficient 的 value 本身。如果 data 没有 normalize ，则一定会由于量纲不一致，产生不同数量级的 $\beta_i$ 。可能有的 $\beta_i$ 因为数量级的缘故非常小但是很重要；有的 $\beta_i$ 因为数量级的缘故非常大。而 Lasso 会 kill 掉这些 coefficient ，RR 也会使这些 coefficient 缩小。因此，必然要对数据做标准化。

Be careful at the very beginning!

What’s more:

Lasso: Powerful to select variables.

RR: Avoid collinearity, weight distributed balancedly.

Reference

本文中的所有图片，Slides均来源于國立台灣大學工業工程學研究所藍俊宏副教授所開設的資料分析方法課程中之 DA04 Dimension Reduction.pdf。特此感謝藍俊宏老師在我學習歷程上的幫助！

1. Curse of dimensionality, Wikipedia ↩︎