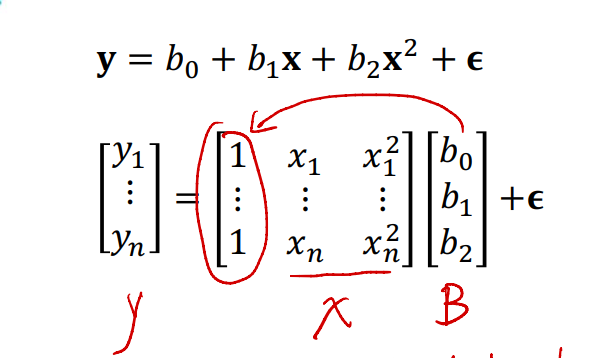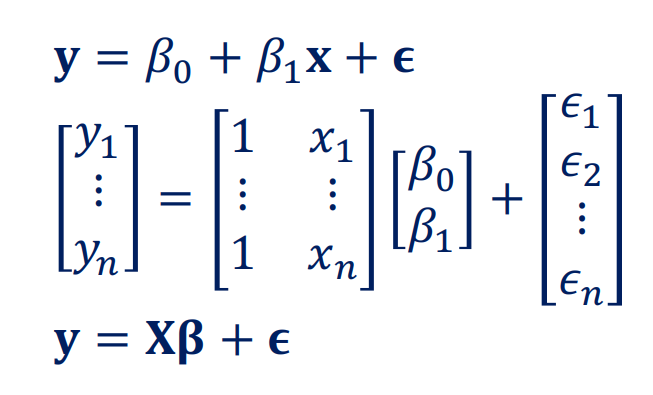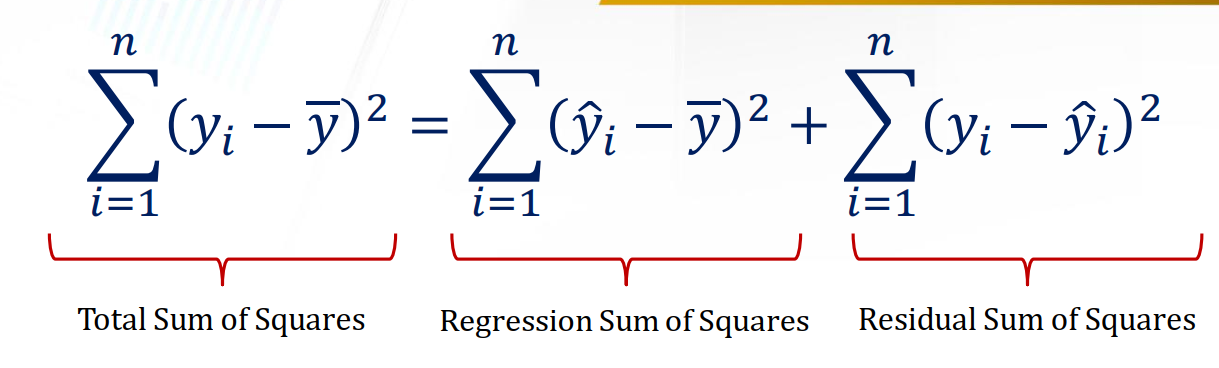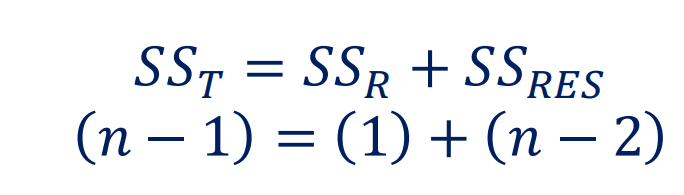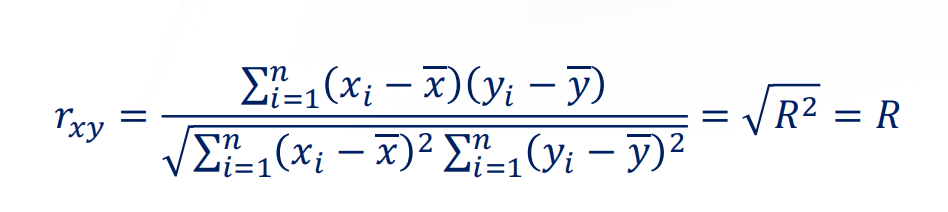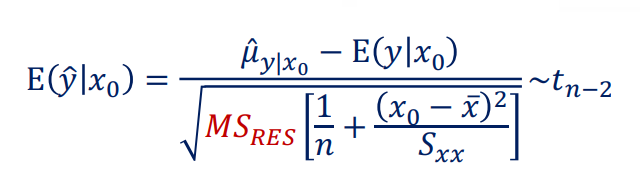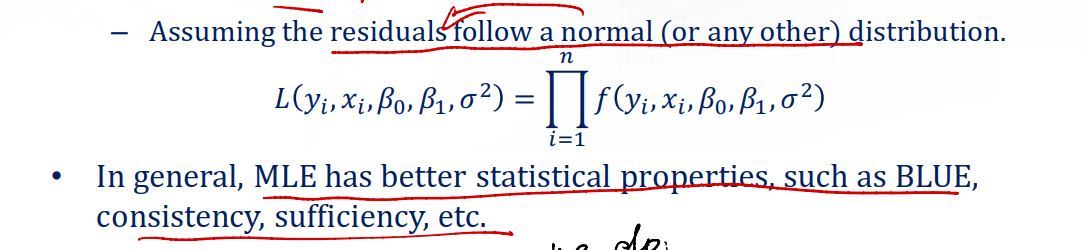DA02 Regression Analysis

DA02 :: Regression Analysis

General Definitions

Here are some basic definitions of linear and linear regression

Linear Relationship

Aim of Linear Regression

我们有类似这样的等式：

\[\left\{ \begin{matrix} \begin{align} & a = b x_1 + cx_2 \\ & d = ex_1 + fx_2 \\ \end{align} \end{matrix} \right.\]

不像线性方程组。在解线性方程组时，我们的目的是已知$a,b,c,d,e,f$求出$x_1$与$x_2$。然而，在linear regression中，我们的目的是通过已经获得的数据，带入到$a,b,c,d,e,f$的位置上，从而估计$x_1,x_2$，也就是所谓的回归系数。

Types of Linear Regression

There are three typical cases:

• Simple Linear Regression
• Multiple Linear Regression
• Multivariate Multiple Linear Regression

Let’s introduce them case by case.

Simple Linear Regression

在Simple Linear Regression中，我们的模型（称为one-one model）大概是：

\[y = a + bx\]

我们的目的是通过数据集，利用一定的方法，估计出参数$a$和$b$。

Multiple Linear Regression

我们的模型大概是：

\[y = a + b_1x_1 + b_2x_2\]

这很像对变量${x_1, x_2, \dots, x_n}$做线性组合（linear combination of variables）。

Multivariate Multiple Linear Regression

在这个线性回归模型中，我们的模型左边不止有一个$y$，还有其他的变量。模型大概是：

\[c_1y_1 + c_2y_2 = a + b_1x_1 + b_2x_2\]

关于线性回归的补充

为什么是线性？

这是因为模型中并不存在线性项。比如，$a_3x_3^2$就是一个典型的非线性项。在线性回归中，它不能出现。

如果有非线性项，该怎么处理？

一个经典的方法是取对数。例如，需要估计$y = x^\alpha$。我们要对其两边取自然对数，构造出：

\[y = x^\alpha \Rightarrow \ln y = a\ln x\]

我们可以对$\ln y$和$ln x$做线性回归。这种处理称为transfer。

Data of Linear Regression

在线性回归中，我们的数据集可以用一个矩阵表示。

\[X_{n \times p} = \left[ \begin{array}{1} x_{11} & x_{12} & \dots & x_{1n} \\ x_{21} & x_{22} & \dots & x_{2n} \\ \dots \\ x_{p1} & x_{p2} & \dots & x_{pn} \end{array} \right]\]

这是一个$n \times p$的矩阵。其中：

• $p$代表着等式右侧的回归变量（variables）个数有$p$个。即${x_1, x_2, \dots, x_p}$。
• $n$代表我们总共抽取了$n$笔资料（samples）。

Purposes of regression

其中，典型包括：

• see relationship between $x$ and $y$.
• see how much $y$ is influenced by $x$.
• seek for a predict value $y$.

Example of Regression Analysis

下面是一个回归分析的例子。从例子中，我们观察如何进行回归分析，如何分析得到的数据。

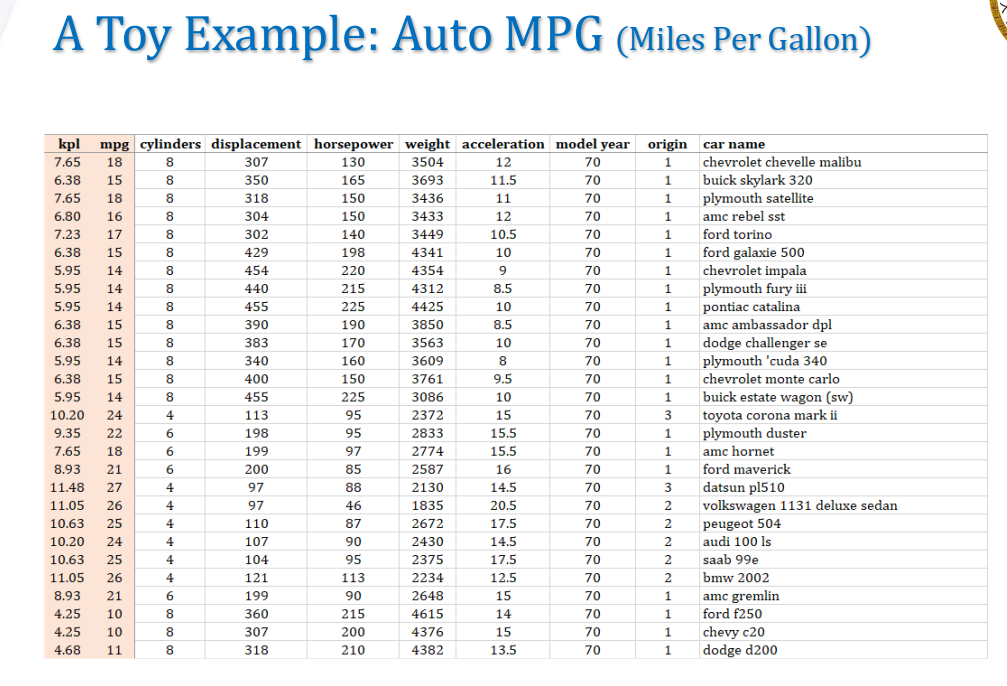
在这个数据集合中，我们有：

• 392笔资料（samples）
• 我们要估测的$y$是左侧的mpg
• 我们有8个variables（即回归中的$x$）

我们的目的是，找出mpg和variables之间的联系。

A Quick View of Data

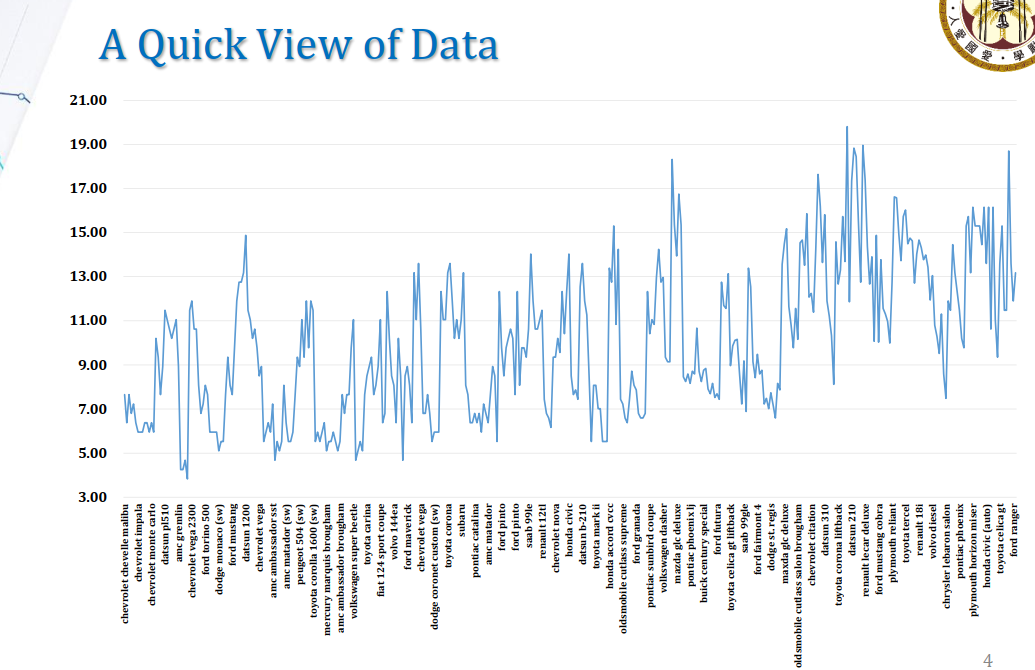
第一步是最重要的：我们要对整个数据进行一个大致的观察。最简单的方式是画一个折线图：

可以发现，mpg似乎随着car models的更新而上升。

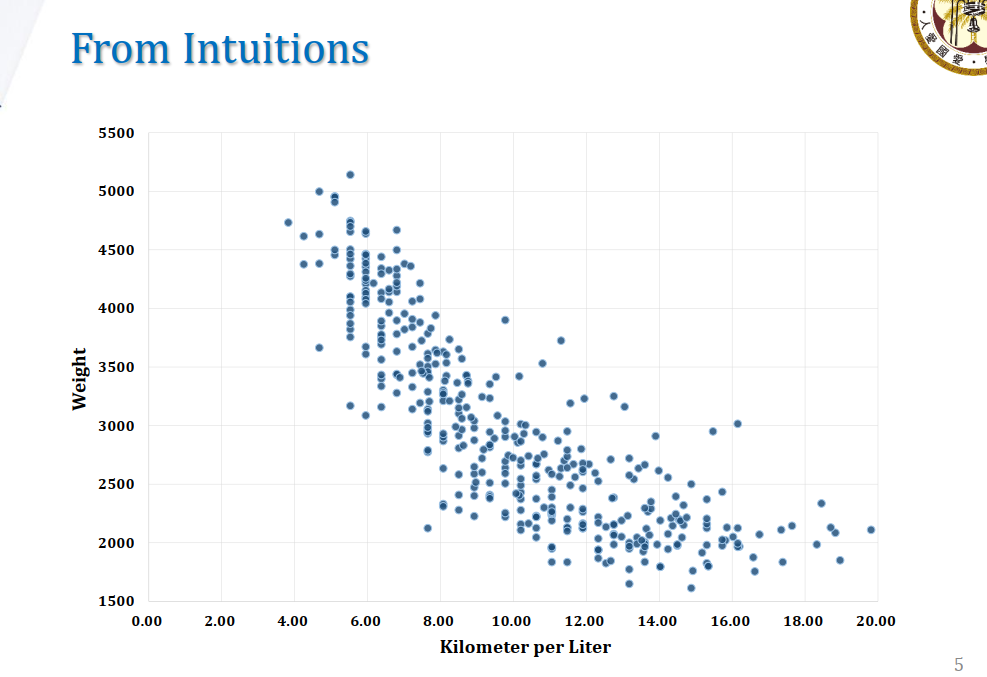
同样，也可以使用散点图（Scatter Plot）进行分析：

可以看出Weight和Kilometer per Liter之间的负相关关系。

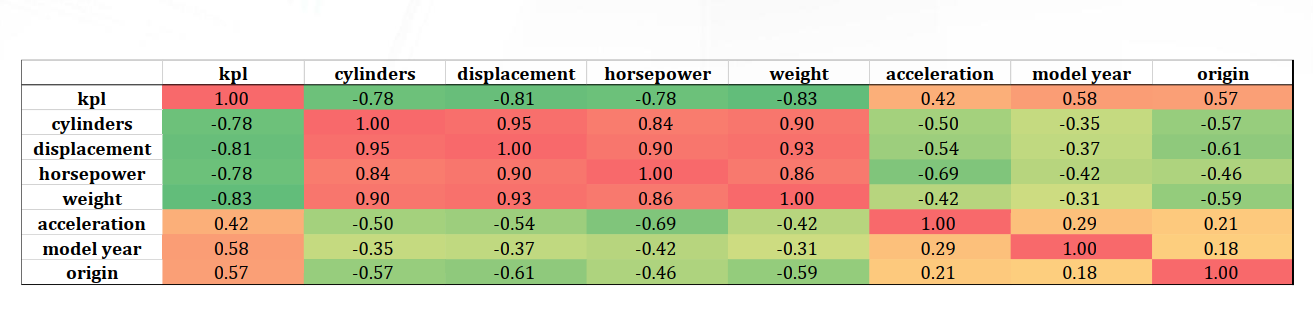
但是，我们很懒不想一个个画图，想迅速看出变量间的相关性，怎么做？$\longrightarrow$利用相关矩阵！

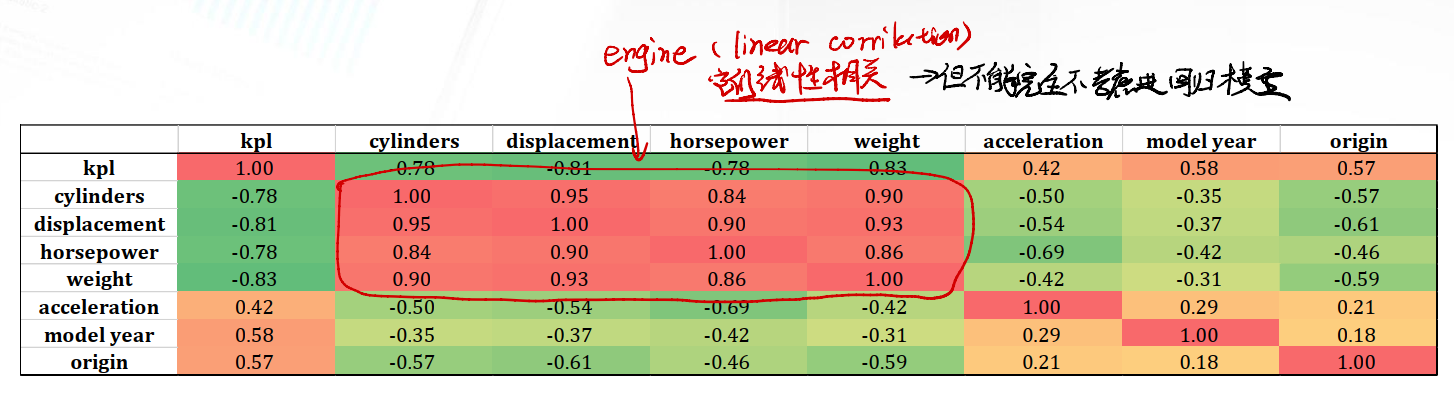
我们将$y$和剩下$x_1, x_2, \dots, x_7$一同做成一个Correlation Matrix。

可以发现：

• cylinders, displacement, horsepower, weight四个部分有高度正相关

下一步，就可以开始regression了。

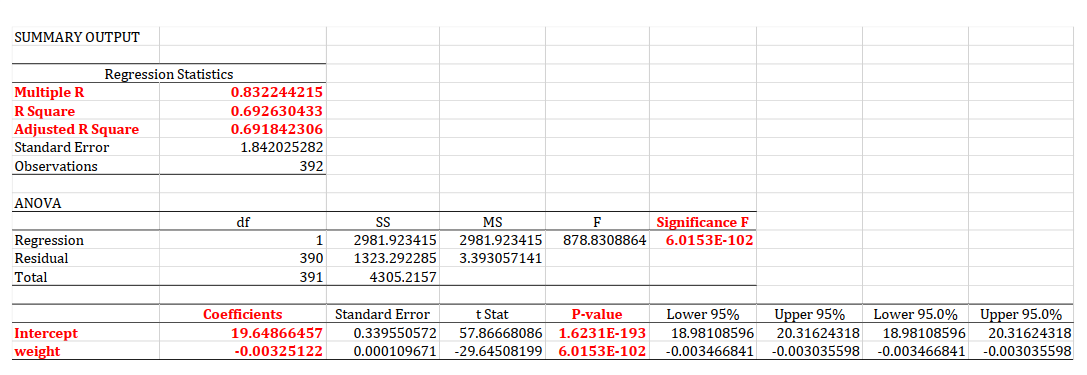
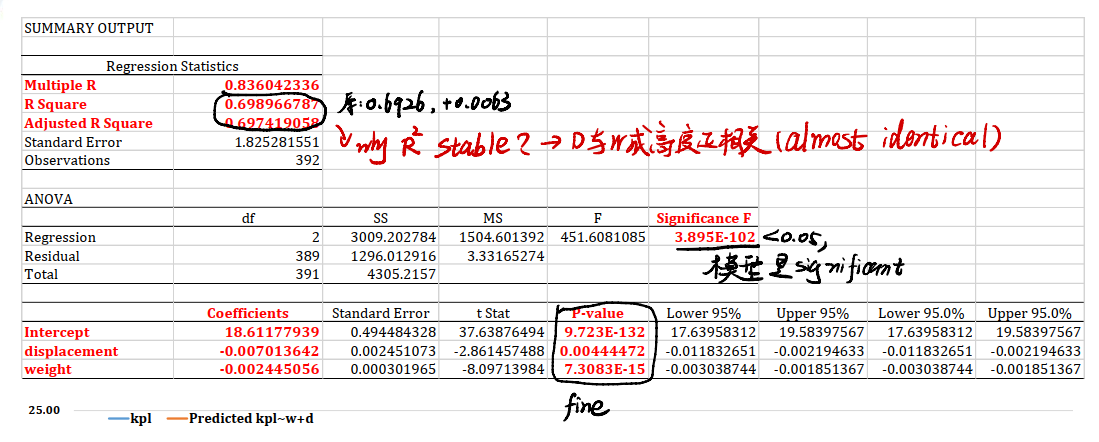
A simple regression between MPG and Weight

现在要对这个表着重研究 :-)

在这个简单回归模型中，我们的模型表达式为：

\[y_{mpg} = b_0 + b_1x_{weight}\]

Regression Statistics Column

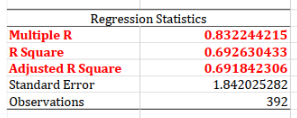
首先看到Regression Statistics这一栏。

• R Square: This shows that we can explain nearly $69.26\%$ of the variation in $y$.
  • However, still nearly $30\%$ variation in $y$ we can not explain yet.
  • If we want to extend the model, we need to find another variable, try to explain the rest $30\%$
  • mind that $0 \leq R^2 \leq 1$.
• Multiple R: This is another $R$ value.
  • Multiple R is $\sqrt{R^2}$.
  • In Simple Regression, $R = COV(x, y)$. However, in multiple regression, it may not hold.
• Adjusted R Square: This is another $R$ value. However, it is effective when conduct multiple regression.
  • Adjusted R Square will punish the number of regression variables. （通过对变量个数进行惩罚，控制模型的规模，从而更好地说明模型的优劣）
  • We shall talk about it later.

ANOVA table in simple linear regression

接下来，注意到下方的ANOVA表格。

在简单线性回归中，我们进行ANOVA分析，主要是检验模型的显著性（Significant or not）。相当于问：Is model valid?我们的ANOVA检验假设为：

\[H_0: b_1 = 0 \\ H_1: H_0\text{ is not true}\]

在这里，假设$H_0$还可以表述为：模型是不显著的。我们做ANOVA分析的目的，就是证明$b_1 \neq 0$。

$b_1 \neq 0$与模型显著有什么关系？

$\rightarrow$ 如果$b_1 \neq 0$，则说明变量$x_1$对模型是有贡献的。说明我们构建这个模型，试图用$x_{weight}$去解释$y_{mpg}$是合理的一种事情。这就是Significant的含义。

ANOVA分析的p-value在表中的Significance F一栏。假设我们选择置信水平$\alpha = 0.05$，可以发现$\text{p-value} < 0.05$。这时候，我们选择拒绝原假设$H_0$（即拒绝模型是不显著的的假设）证明我们构建的模型在统计上是显著的，可以用变量$x_{weight}$去解释$y_{mpg}$。模型的合理性得到了解释。

The last table

最后一个表格是在下方，给出了回归分析的结果。

• Coefficients：这一栏给出了回归分析得出的系数值。
  • Intercept：截距项。在我们的模型中其实就是$b_0$的值。
  • weight：表示$x_{weight}$这一变量对应的系数值。其实就是模型中的$b_1$。
• p-value：在这一部分，我们还要对每个系数单独做检验，验证其是否显著（也就是验证是否某系数为$0$）。

因此我们的模型最终可以写为：

\[y_{mpg} = 19.65 + (-0.003)x_{weight}\]

为什么weight的系数很小？

$\rightarrow$ 这要从两个变量的数量级分析。从数据集中可以看出，mpg的值大概分布在$[10, 30]$之间，而weight的值一般都有四位数。双方差距过大，导致了weight的回归系数较小的结果。

p-value的假设？

$\rightarrow$ 在这个假设检验中，我们分别对$b_0$与$b_1$做假设：

\[H_0: b_0 = 0 \\ H_1: H_0 \text{ is not true}\] \[H_0: b_1 = 0 \\ H_1: H_0 \text{ is not true}\]

其实就是分别检验两个回归系数是否为0。

Why ANOVA Test?

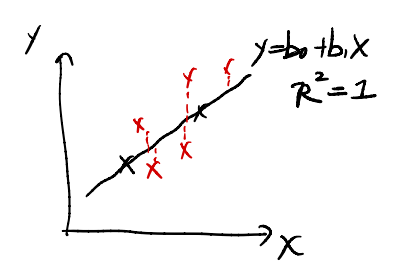
最后一个问题是，为什么要用ANOVA分析来验证模型是否准确？考虑下面的这幅图：

假设数据集一开始只有两个点，用黑色表示。可以发现，两个点进行回归，其$R^2 = 1$。

然而这个模型必然不准确。随着搜集的资料数目越来越多（上图红色点），模型的误差将会越来越大，这时：

1. $R^2$不会为1，并且$R^2 \downarrow$。因此我们不能简单地用$R^2$来描述模型的好坏。本例中虽然$R^2$有所下降，但是模型针对新加入的资料进行调整，毫无疑问是一件好事情，模型变好了。
2. ANOVA Test会拒绝$b_1 = 0$的原假设，我们从而可以进行模型的validate。

What next?

在进行了简单的分析后，我们肯定希望进行复杂的分析。比如扩充模型的变量数目。回到之前的Correlation Matrix:

我们可以考虑将cylinders, displacement, hoursepower等变量加入模型中一起考虑。虽然这些变量都有高度的线性相关性，但这并不意味着我们无需将其纳入回归模型中。正确的做法是先回归，随后用假设检验的方法检验每个变量系数是否为0。

Next Move: MPG ~ Weight + Displacement

现在我们扩充模型，将displacement这一变量纳入回归中。我们的模型可以写为：

\[y_{mpg} = b_0 + b_1x_{w} + b_2x_d\]

在这个multivariable regression analysis model中，我们有了三个待估计参数$b_0, b_1, b_2$.

一样，得到一张如下的表格：

Regression Statistics

这里又存在几个新的问题：

• R Square的值：在上一个回归模型中，$R^2 = 0.6926$，而本模型中$R^2 = 0.6989$。虽然加入了一个新变量，但$R^2$居然没有显著的提升…
  • 这是因为，我们之前提到过的相关矩阵中，weight和displacement两个变量呈现着高度的正相关性。因此加入displacement，模型并不会有特别显著的提升。
• 在ANOVA分析中，可以证明模型是显著的。
• 然而，前面埋的雷会在最下方的p-value中得到体现。
  • displacement的p-value数量级很大，是0.0044；而weight的数量级很小，大概是$10^{-15}$这个级别。这也从侧面说明我们新加入的displacement系数虽然在$95\%$甚至$99\%$的置信水平下，虽然可以拒绝原假设$H_0$，但displacement的影响着实是微乎其微。

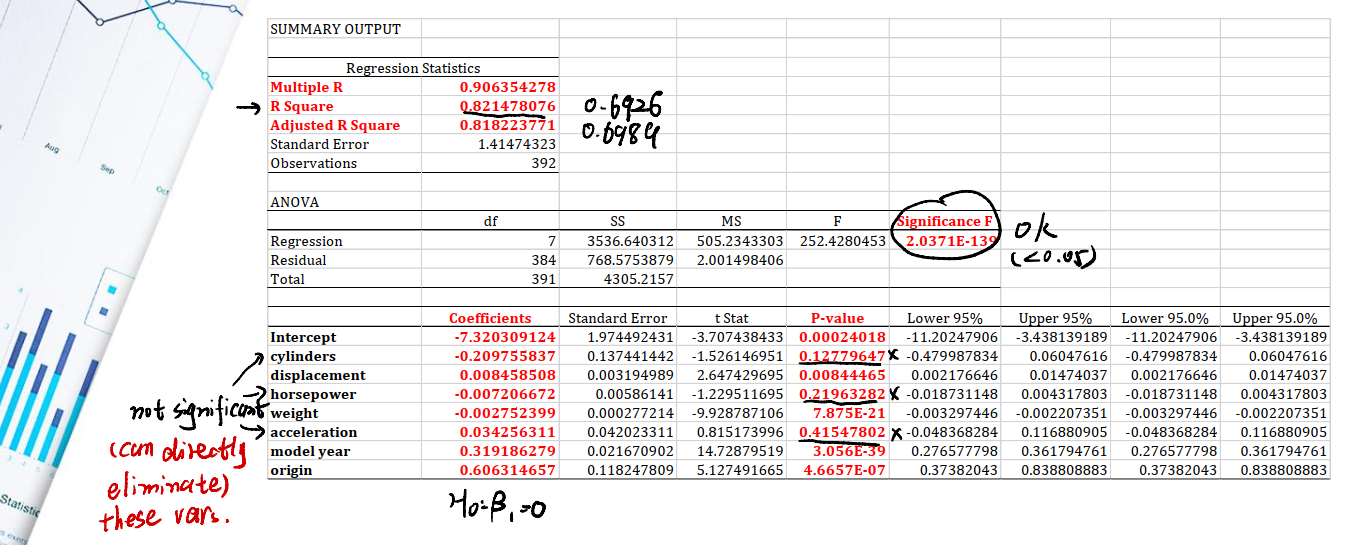
All-in Model

现在把其他的几个变量都拿进来做一个回归：

Regression Statistics

• 确实加入了几个新变量，$R^2$有了明显的提升。从0.6926提升到了0.8214。证明模型正在变好。

ANOVA

• Significant F的值很小，说明all-in的模型是显著的。

Coefficients

• 注意到p-value这一栏，cylinders, horsepower, acceleration三个变量的p-value都大于我们的置信水平0.05，这意味着它们并未通过检验，说明三个变量在模型中起到的贡献非常小，可以将其eliminate。

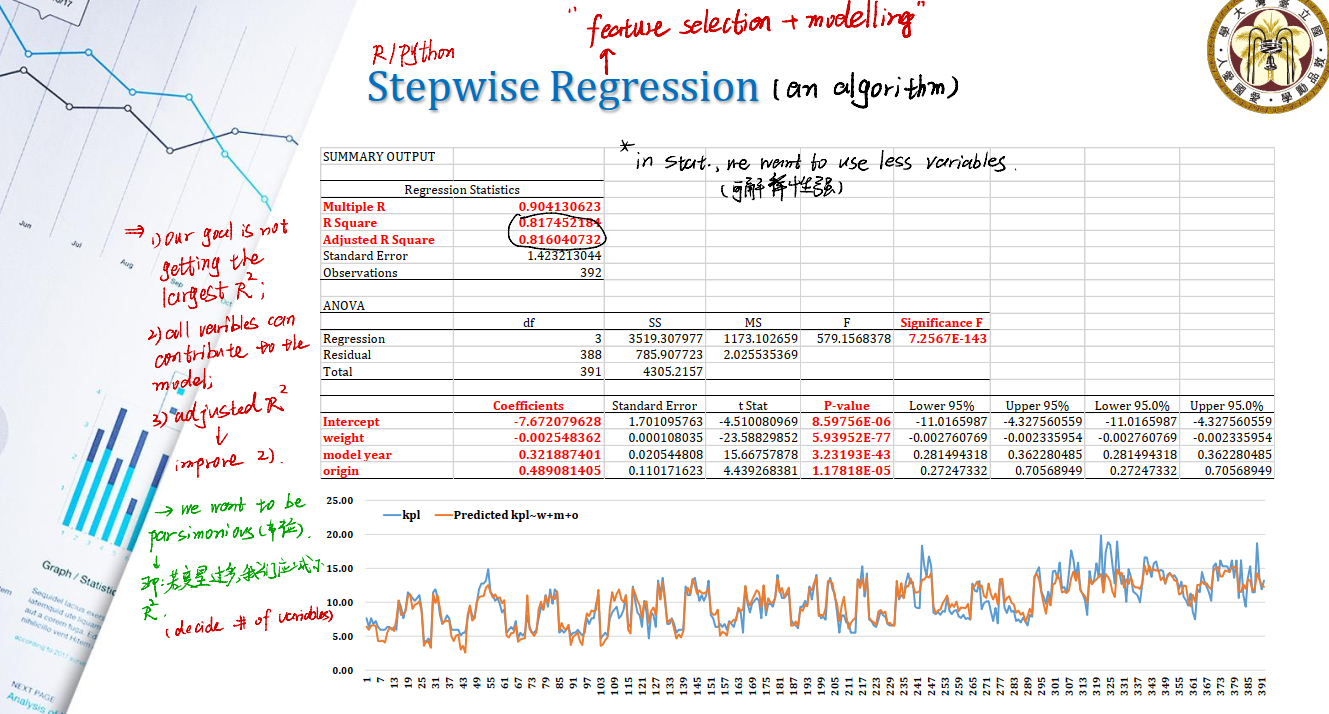
Stepwise Regression

Why Stepwise Regression?

1. Our goal is not getting the largest $R^2$
2. All variables can contribute to the model
3. So, we shall use adjusted R Square to improve 2.

核心思想就是，我们希望用最少个数的变量来构建模型。这样的模型具有较强的可解释性。我们希望用adjusted R Square来作为新的衡量。这也是一种trade-off。

Regression is Linear

回到linear的问题上。怎么用一个线性模型来估计非线性数据集？

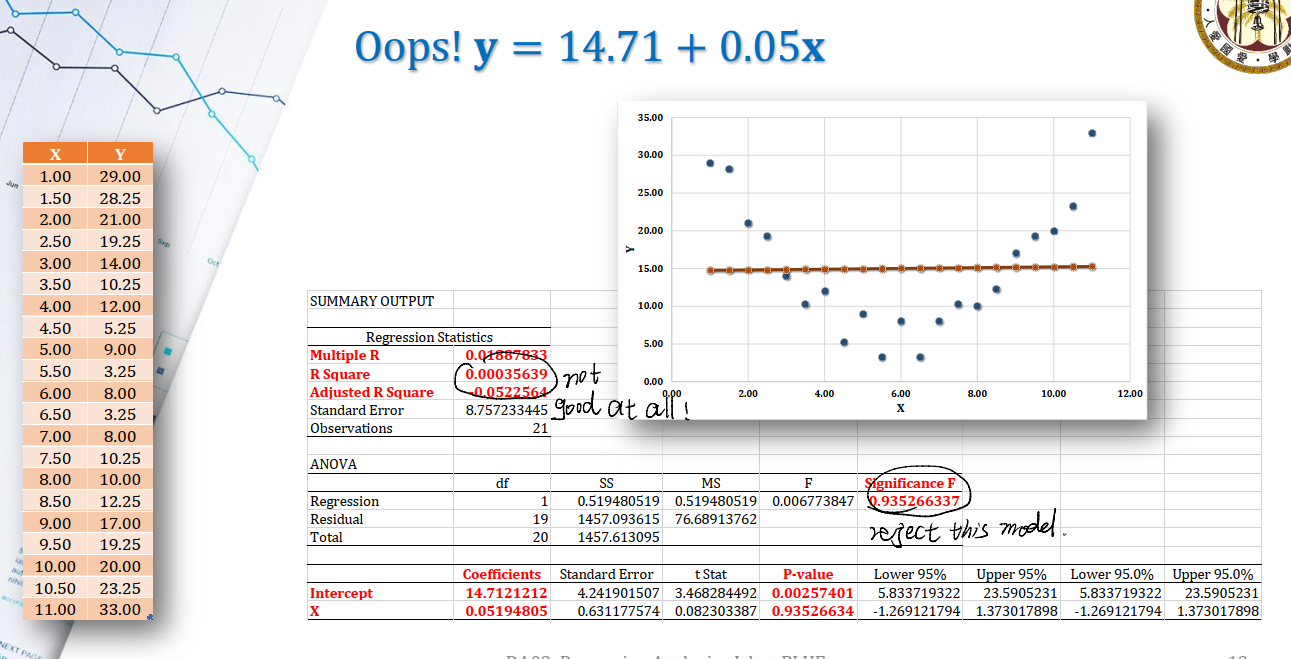
假设我们有一个数据集，我们试图用一个$y = b_0 + b_1x$来进行回归：

如果简单采用一次项来估计，效果很差，并且ANOVA分析也无法通过。

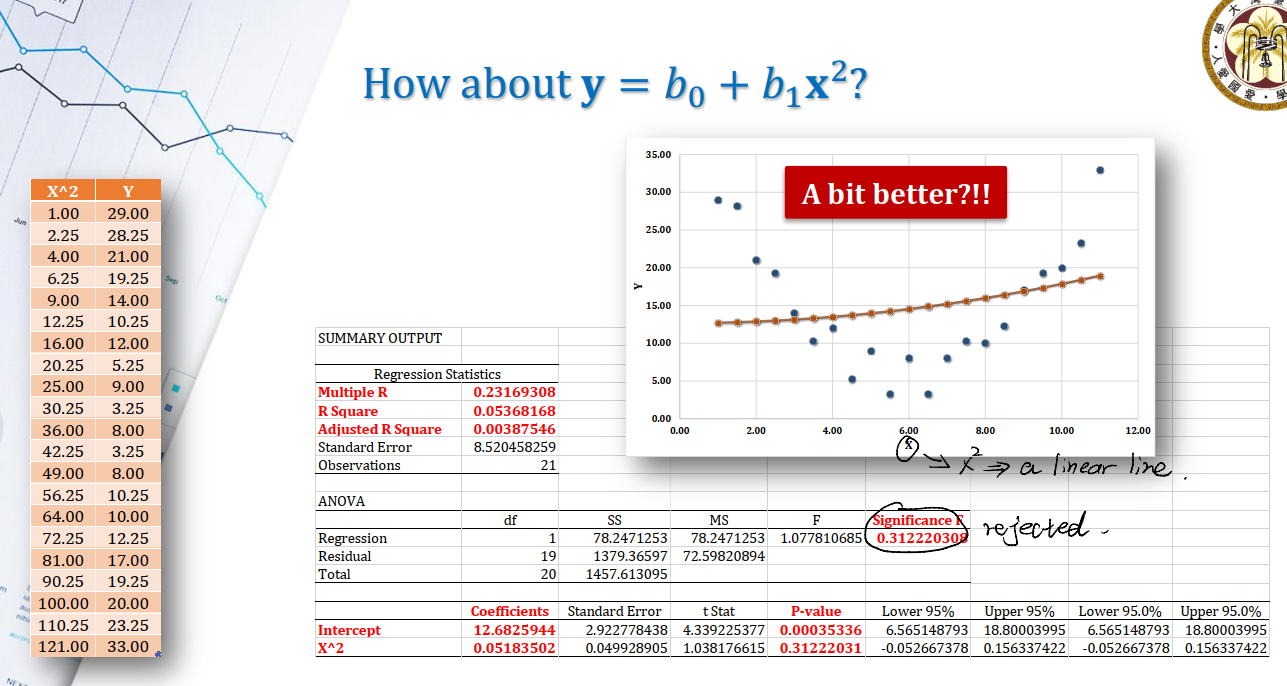
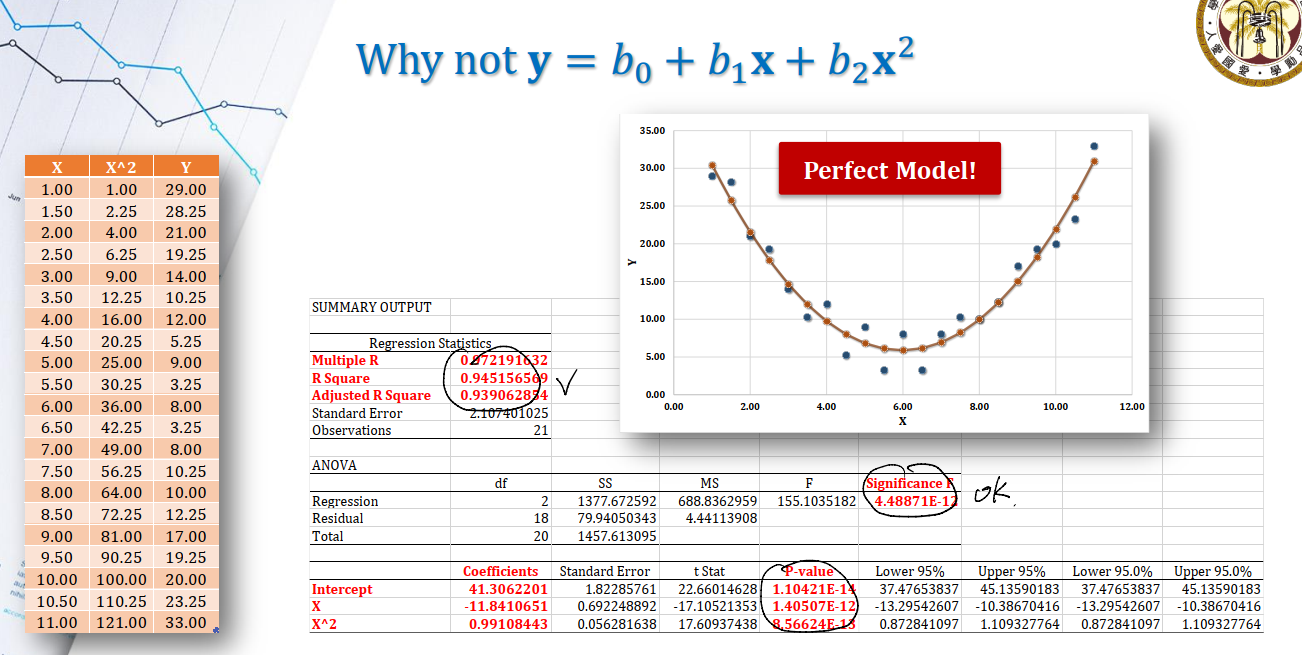
二次项也是同理。我们自然想到用$y = b_0 + b_1x + b_2x^2$来估计。

所以现在的问题是，这到底是不是一个linear model？

Linear or not

我们的新模型为：

\[\mathbf{y} = b_0 + b_1\mathbf{x} + b_2 \mathbf{x^2} + \epsilon\]

如果我们考虑矩阵形式：可以发现这相当于用$b_0, b_1, b_2$对$x, x^2$进行linear combination。可写成：

其中：

• $x_1 , \dots, x_n$是我们抽取的$n$笔资料，对应的是$y_1, \dots, y_n$
• $b_0, b_1, b_2$是把$1, x_1, x_2^2$进行线性组合的系数
• $\epsilon$称为residual，假设服从正态分布$N(0, \sigma^2)$

模型可记为：

\[\mathbf{y} = \mathbf{X}\mathbf{\beta} + \epsilon\]

而在估计式上，我们可以记为：

\[\hat{\mathbf{y}} = \mathbf{X} \hat{\mathbf{\beta}}\]

• $\hat{y}$代表$y$的predict value。
• $\hat{\beta}$代表我们通过回归的方法得到的回归系数。
• 没有$\epsilon$是因为，我们根本无法预测一个完全随机的误差$\epsilon$。

Estimate regression coefficient: Least Squares Estimator(LSE)

一个经典的方法是最小二乘法。

在之前，我们已经有：

\[\hat{\mathbf{y}} = \mathbf{X} \hat{\mathbf{\beta}}\]

由$y = x\beta + \epsilon \Rightarrow \epsilon = y - x\beta$。从而：

\(\epsilon = [\epsilon_1, \epsilon_2, \dots, \epsilon_n]\) 因而可以写出残差的Sum of Square：

\[S(\mathbf{\beta}) = \sum^{n}_{i = 1}\epsilon_i^2 = (y - x\beta)^T(y-x\beta) = y^Ty - 2\beta^TX^Ty + \beta^TX^T + \beta^TX^TX\beta\]

$S(\beta)$被称为residual sum of square。

我们做LSE，目的是最小化$\text{SS}_{residual}$。对$S(\beta)$求关于$\beta$的偏微分：

\[\frac {\partial S} {\partial \beta} = -2X^Ty + 2X^TX\hat{\beta} = 0\]

得：

\[X^Ty = X^TX\hat{\beta}\]

从而求出最小二乘估计下的$\beta$为：

\[\hat{\beta} = (X^TX)^{-1}X^Ty\]

这就是最小二乘（LSE）估计下的回归系数$\beta$的估计值$\hat{\beta}$。

Hint：一定要检查$X^TX$是否可逆！

A Geometric Interpretation of LSE

现在我们从几何的角度试图理解LSE的原理。我们已经知道，对$y$而言，其是一个$y_{n_\times1}$的向量。而对$X$而言，其是一个$X_{n \times p}$的矩阵。

从回归的角度而言，我们的目的是将$n$笔资料，投影到一个$p$维的空间，从而求出$\beta_{p\times1}$。注意到资料的数目一般而言是远远多于回归变量$x$的数目。我们自然可得$n » p$。

1. 在矩阵$X$中，其Column Space是至多$p$维的；而$y$是一个$n$维的向量。所以矩阵$X$的列空间是一个$n$维空间的子空间。
2. 如果$p$个向量线性独立（即$x_1, x_2, \dots, x_p$线性独立），则肯定可以span成一个$p$维空间。
3. 所以在回归分析中，我们的本质是，期望用一个小维度的空间$p$（也就是$p$个回归变量$x$），以及$n$笔资料，来解释一个高维度空间（这个高维度空间就是$y$）。从而求得回归系数的向量$\beta$。

依照之前，我们有：

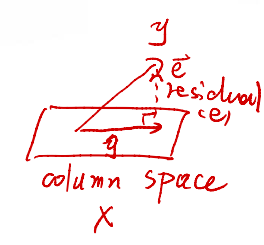
\[\hat{\beta} = (X^TX)^{-1}X^Ty \\ \hat{y} = X\hat{\beta} = X(X^TX)^{-1}X^Ty\]

现在来思考几何意义。如上图：

• 平面是$X$的列空间。这个列空间的维度是$p$。
• 向量$\mathbf{y}$是$n$维的向量，因此不可能在$X$的列空间中，画成一个指出去的向量。$y$应该在$\mathbb{R}^n$空间内。

但我们只能在$X$的列空间中找（因为我们只有变量$x_1, x_2, \dots, x_p$，它们张成的空间最大维度也就是$p$维）。那我们只能进我们的努力，找到一个所谓的与y最接近的向量，这就是我们对$y$的回归估计值$\hat{y}$。它就是$X\hat{\beta}$。

所以，在$X$的列空间中，哪一个向量是与$y$最接近的？当然是所谓的正交投影。这样我们就找到了一个$p$维的向量。我们就把它当成$y$。

然而，这里存在维度上的损失，因为$n » p$。所以我们会有一个残差residual，记为$e$。$e = y - \hat{y}$。注意这里是向量相减，所以表现成所谓垂直的向量。这也就是投影和实际的差距。

Collinearity的影响

我们经常听说所谓的多重共线性。那多重共线性会有什么影响？

在之前，我们有$\hat{y} = X(X^TX)^{-1}X^Ty$。在向量中，我们知道$(X^TX)$代表的是一个矩阵的Center。

如果出现共线性，以$x_1, x_2, x_3$为例，有：

\[x_1 = a_1x_2 + a_2x_3\]

这意味着$x_1$是replaceable的。可以被$x_2,x_3$替代。如果出现多重共线性，以$\mathbf{X}_{3 \times 3}$为例：

\[\mathbf{X}_{3 \times 3} = \left[ \begin{array}{1} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{array} \right]\]

这个时候会发现，由于$x_1$与$x_2, x_3$互相线性相关，$\mathbf{X}_{3 \times 3}$的Column Space是不满秩的！考虑到矩阵相乘相当于做一个linear transform，矩阵的秩只可能减少或者不变。从而会有$\text{rank}(X^TX) < p$。因此回到之前$\beta$的估计式，会导致：

\[\hat{\beta} = (X^TX)^{-1}X^Ty\]

中的$(X^TX)^{-1}$不存在！进而无法进行最小二乘估计。

因此实务上我们要检验多重共线性，防止出现无法使用最小二乘的情形。

从几何的角度，相当于$\mathbf{X}$的$p$个变量无法张成$p$维的空间。

Scientific Details inside the regression

在这一部分，我们将介绍一些regression中的重要条件以及问题，并给出解决问题的方案。

Linear Assumptions in Simple Regression

在简单线性回归中，我们有：

\[\begin{align*} y_1 & = \beta_0 + \beta_1x_1 + \epsilon_1 \\ y_2 & = \beta_0 + \beta_1x_2 + \epsilon_2 \\ \vdots & \\ y_n & = \beta_0 + \beta_1x_n + \epsilon_n \end{align*}\]

在模型$y = x\hat{\beta} + \epsilon$中：

• $\hat{\beta}$是我们可以估计的值
• $\epsilon$是一个random noise，我们无法估计，这也是$y$的随机性的来源

因此，对于一个简单线性回归模型，我们有linear assumptions:

1. $E(\epsilon_i) = 0, \text{for all } i = 1, 2, \dots, n$
2. $var(\epsilon_i) = \sigma^2, \text{for all } i = 1, 2, …, n$
3. $cov(\epsilon_i, \epsilon_j) = 0, \text{for all } i \neq j$

其中，条件2的$\sigma^2$是一个定值，我们称这种条件交stationality，即稳定性。

当然，我们也有与其等价的以$x_i, y_i$表述的equivalent assumptions:

1. $E(y_i) = \beta_0 + \beta_1x_i, \text{for all } i = 1, 2, \dots, n$
2. $var(y_i) = \sigma^2, \text{for all } i = 1, 2, \dots, n$
3. $cov(y_i, y_j) = 0, \text{for all } i \neq j$

所以，矩阵形式呢？

Matrix Form Assumptions

我们有：

linear assumptions:

1. $E(\mathbf{\epsilon}) = 0$
2. $cov(\epsilon) = \sigma^2 \mathbf{I}$

Equivalent Assumptions:

1. $E(y) = X\beta$
2. $cov(y) = \sigma^2 \mathbf{I}$

Questions to Understand Regression

Let’s answer them one-by-one.

Question #1: Estimate parameters

我们可以利用最小二乘法来对参数进行估计。

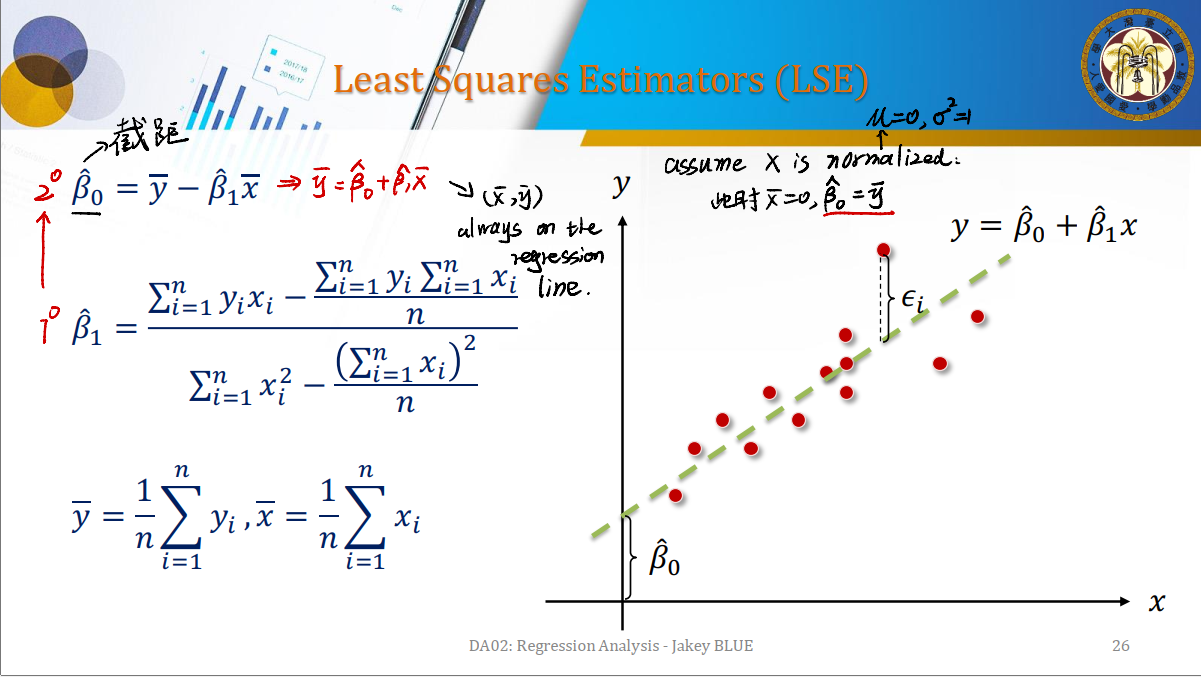
联立上图得到的Normal Equations，即可求出$\hat{\beta_0}, \hat{\beta_1}$。

这里还有两个特殊的性质需要知道：

1. $(\bar{x}, \bar{y})$ 永远在回归线上。
2. 如果数据集$X$已经被标准化（normalized），即$\mu = 0, \sigma^2 = 1$，会有：
3. $\bar{x} = 0$
4. $\hat{\beta_0} = \bar{y}$

同样地，经过变形有：

\[\hat{\beta_1} = \frac {\sum^n_{i = 1} (y_i - \bar{y})(x_i - \bar{x})} {\sum^n_{i = i}(x_i - \bar{x})^2}\]

我们称$S_{xy}$为变量$x$与变量$y$的离均差乘积之和，称$S_{xx}$为变量$x$的离均差乘积。可以将$\beta_1$改写为$S_{xy} / S_{xx}$。

另外，我们还可以通过之前的linear assumptions得出一些性质。

• $E(\epsilon_i) = 0 \Rightarrow \sum^{n}{i = 1}(e_i) = 0 $, $ \Rightarrow \sum^{n}{i = 1}(y_i - \hat{y_i}) = 0$，从而有 $\sum^n_{i = 1} \hat{y_i} = \sum^n_{i = 1} {y_i}$ 。
• 数据的centroid 总是在regression line上。
• 联系之前的回归几何意义，我们可以得出：
  • $\sum^n_{i = 1} x_ie_i = 0 \iff X^Te = 0$。由于$\vec{e}$总是与$X$的Column Space垂直，可以得到。
  • $\sum^n_{i = 1} \hat{y_i}e_i = 0 \iff \hat{y}^Te = 0$。由于我们是在$X$的Column Space中选择一个投影$\hat{y}$，故其与$\vec{e}$也必然垂直。

Question #2: Unbiased LSEs

可以证明，$\hat{\beta_1}$和$\hat{\beta_0}$都是无偏估计量。

考虑LSE估计量的方差：

\[Var(\hat{\beta_1}) = \frac {\sigma^2} {S_{xx}} \\ Var(\hat{\beta_0}) = \sigma^2 (\frac {1} {n} + \frac{\bar{x}^2} {S_{xx}})\]

Gauss-Markov Theorem: LSEs are unbiased and have minimum variance. If linear assumptions are satisfied in the regression model.

Question #3: Test of Significance of LSEs

Our target is testing whether $\beta_0 = 0$ and $\beta_1 = 0$. If we want to test the significance, we shall add two more assumptions:

• $\epsilon_i \sim N(0, \sigma^2)$
• $y_i \sim N(\beta_0 + \beta_1x_i, \sigma^2)$

Then we need to conduct two tests individually.

注意到这里我们出现了一个$\hat{\sigma}$。这是一个我们需要估计的参数。会在Question #4提到。同时，也要考虑到sample size。如果是小样本量，我们可以用t分布检验；大样本量，我们可能需要用正态分布来检验。

Question #4: Estimating $\sigma$ by $\hat{\sigma}$

As we have already known, our model is $y = x\beta + \epsilon$, and $\epsilon \sim N(0, \sigma^2)$. So, $\sigma$ is a nature noise we can not estimate in the data. How can we estimate it?

$\rightarrow$ We shall obtain $\hat{\sigma}$ from the residual sum of squares.（残差平方和）

\[SS_{res} = \sum^n_{i = 1}(y_i - \hat{y_i})^2 = SS_T - \hat{\beta_1}S_{xy}\]

其中，$SS_T$（Total Sum of Square）的计算式为：

\[SS_T = \sum_{i = 1}^n (y_i - \bar{y})^2\]

We can get,

\[\hat{\sigma^2} = \frac {SS_{RES}} {n - 2} = MS_{RES}\]

where $MS_{RES}$ is called Residual Mean Square. We can use it to estimate $\sigma^2$. There are two properties of $\hat{\sigma^2}$:

• $E(\hat{\sigma^2}) = \sigma^2$ is an unbiased estimator,
• $\hat{\sigma}$ is also known as the standard error of the regression model.

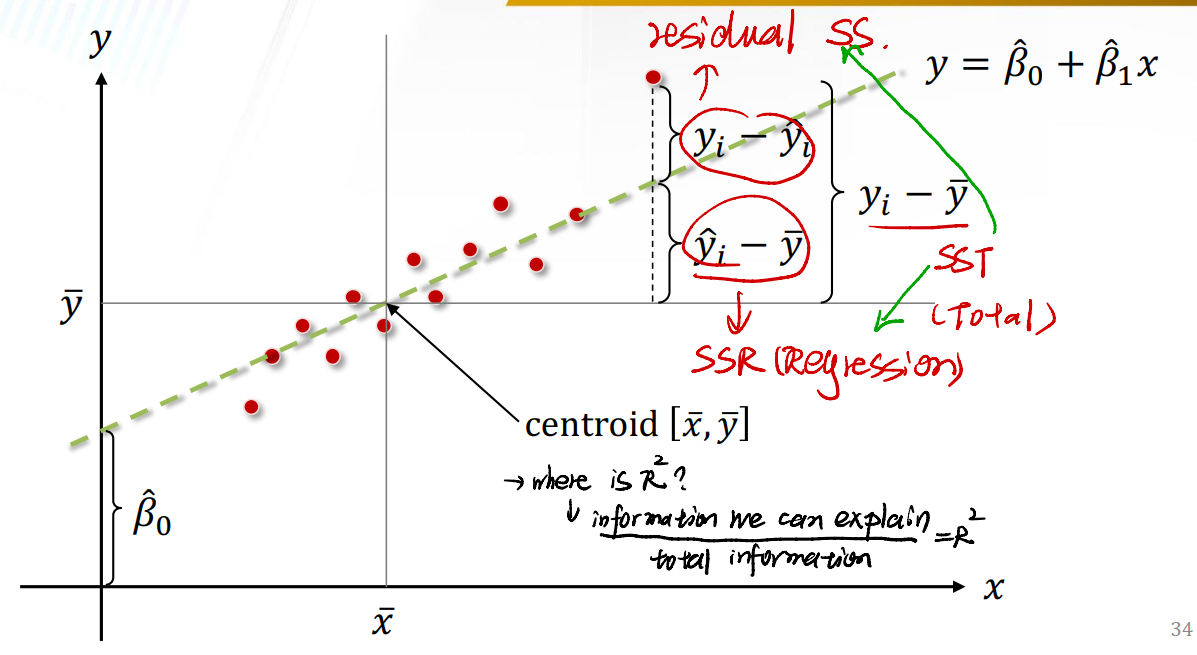
Decomposition of the Sum of Squares

现在我们试图对这几个SS（Sum of Square）进行分解：

• Regression Sum of Squares: 这部分是我们的回归模型的误差。表达的是在给定的$\bar{y}$下，我们试图explain$x$。它可以用来衡量我们的回归模型距离数据集的中心（也就是$\bar{y}$）有多远。
• 为什么要有Regression Sum of Squares？$\rightarrow$我们通过回归模型计算得到的$\hat{y}$很可能是不准确的，我们希望知道我们能解释多少$y$。（explain how much we can explain $y$）

自由度也被分解为了两个部分：

Graph Illustration:

• 回归直线与$\bar{y}$之间的差值是SSR(Regression Sum of Square)。
• 数据点和回归直线之间的差值是SSr(Residual Sum of Square)。
• 数据点和$\bar{y}$之间的差值是SST(Total Sum of Square)。

So what is the meaning of $R^2$?

\[R^2 = \frac {\text{information we can explain via regression model}} {\text{total information in the dataset}}\]

Question #5: Model is Significant? ANOVA

模型是否显著的问题，其实就是检查模型的回归系数$b_0 = b_1 = \dots = b_n = 0$的问题。我们直接利用ANOVA即可分析。

当然，我们并不是检查是否每个系数都不为0。只要证明不全为0，我们的模型就是统计意义上显著的。

Question #6: $R^2$ for what?

$R^2$ is called Coefficient of Determination, indicating the percentage of the variability explained in the regression model.

\[R^2 = \frac {SS_R} {SS_T} = 1 - \frac {SS_{RES}} {SS_T}\]

• $SS_R$: Regression Sum of Square
• $SS_T$: Total Sum of Square
• $SS_{RES}$: Regression Sum of Square

However, how high is high enough? We shall think it carefully…

$R^2$ is always increasing if we keep putting new regressors into the model. So we need to constraint the number of regressors.

$\rightarrow$ Adjusted $R^2$: To correct the inflation of $R^2$

\[R^2_a = 1 - \frac {SS_{RES} / n - 2} {SS_T / n - 1} = 1 - (\frac {n - 1} {n - 1 - 1})(1 - R^2)\]

Adjusted $R^2$可以改善因为增加回归变量导致的$R^2$不断增大的情况。

Question #7: What is $R^2$? The Square Root of $R^2$

In Simple Regression, 𝑅 means the (Pearson’s) correlation coefficient between the $x$ and $y$.

\[R^2 = \frac {SSR} {SST} = \frac {\beta_1 S_{xy}} {SS_{yy}} = \frac {S^2_{xy}} {S_{xx} S_{yy}} = \frac {cov(x, y)} {\sqrt{var(x)} \sqrt{var(y)}}\]

where $SS_{yy}$ is the sum square of $y$.

Question #8: How Confident is the Model?

我们有条件期望：

\[E(\hat{y} | x_0) = \hat{\mu}_{y|x_0} = \hat{\beta_0} + \hat{\beta_1}x_0\]

其中，$x_0$是用来拟合模型的原始数据集中$x$取值范围的任何一个值。

对$\hat{y} \lvert x_0$求条件方差：

\[V(\hat{y} \lvert x_0) = V(\hat{\beta_0} + \hat{\beta_1}x_0) = V(\bar{y} + \hat{\beta_1}(x_0 - \bar{x}))\]

这说明，如果$x_0$距离$\bar{x}$（即数据集$x$的中心）越远，则估计的方差会$\uparrow$。

\[V(\hat{y} | x_0) = \frac {\sigma^2} {n} + \frac {\sigma^2 (x_0 - \bar{x})^2} {S_{xx}} = \sigma^2[\frac {1} {n} + \frac {(x_0 - \bar{x})^2} {S_{xx}}]\]

这也说明了方差增加的原因。（$x_0$距离$\bar{x}$（即数据集$x$的中心）远）

我们进而可以求出条件方差$E(\hat{y} \lvert x_0)$的机率分布：

有了分布，我们也可以根据给定的置信水平，来求取一个置信区间：

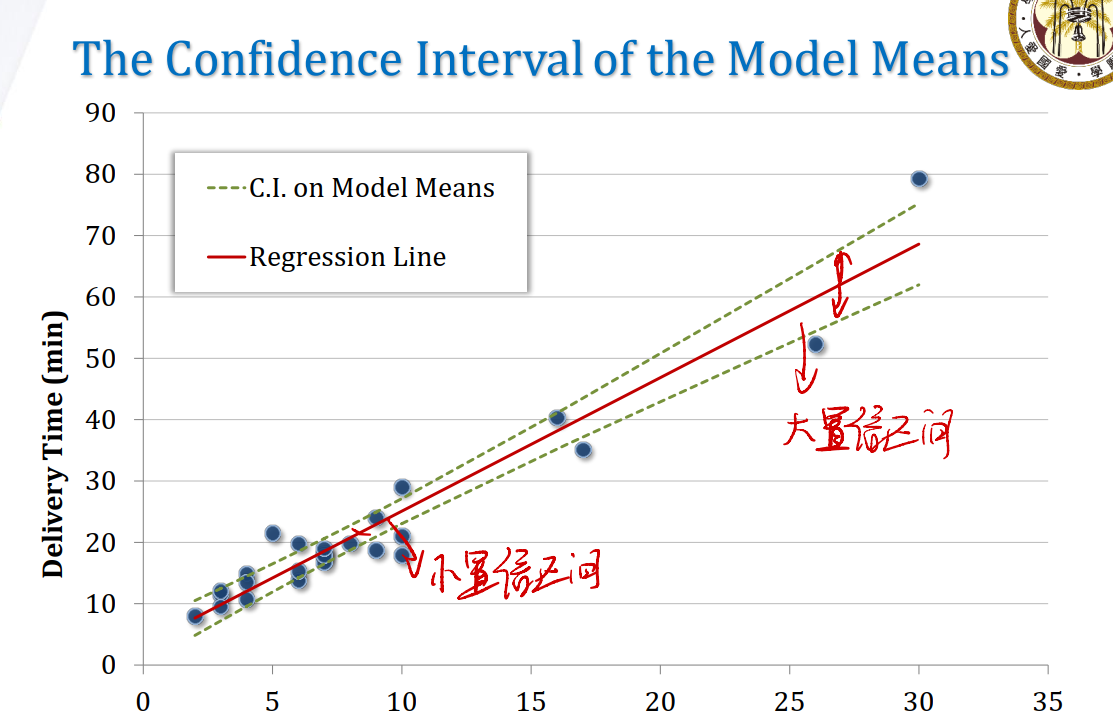
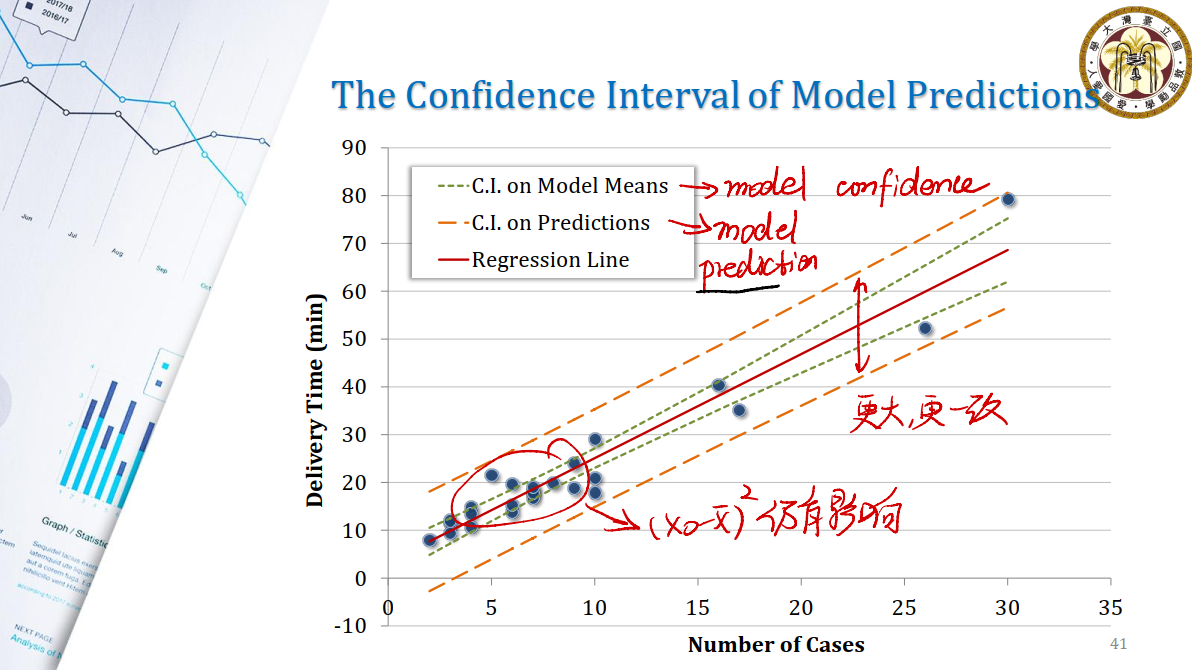
从图像的角度来看置信区间：

• 数据集越大，置信区间越宽（因为我们有了更多分布不同的数据，这些数据都受到了nature noise $\epsilon$的影响）。如下图所示

Question #9: The Precision of the Model Predictions

Precision: 模型预测的值是否在一个范围之内，可以用方差来衡量。

Predictions: 模型的预测精度，即正确率。

我们用$y_0 - \hat{y_0}$作为预测变量，来观察其分布。

可以看出：

• 用Model means来刻画模型的confidence，即我们相信数据大致分布在什么区间内。
• 用Predictions来刻画模型的prediction。
• 随着模型数据集的增大，Model Means线和Predictions线更加一致。

Question #10: Is LSE the only way?

Not really. We shall use most likelihood estimation.

Conclusion

One More Thing: Bias-Variance Trade-off

我们经常会遇到一个问题：到底是该让模型追求准确，还是让模型变得更加适用（即能产生一个相对准确的分布）。下面的示例会让我们更加直观地认识这个问题。

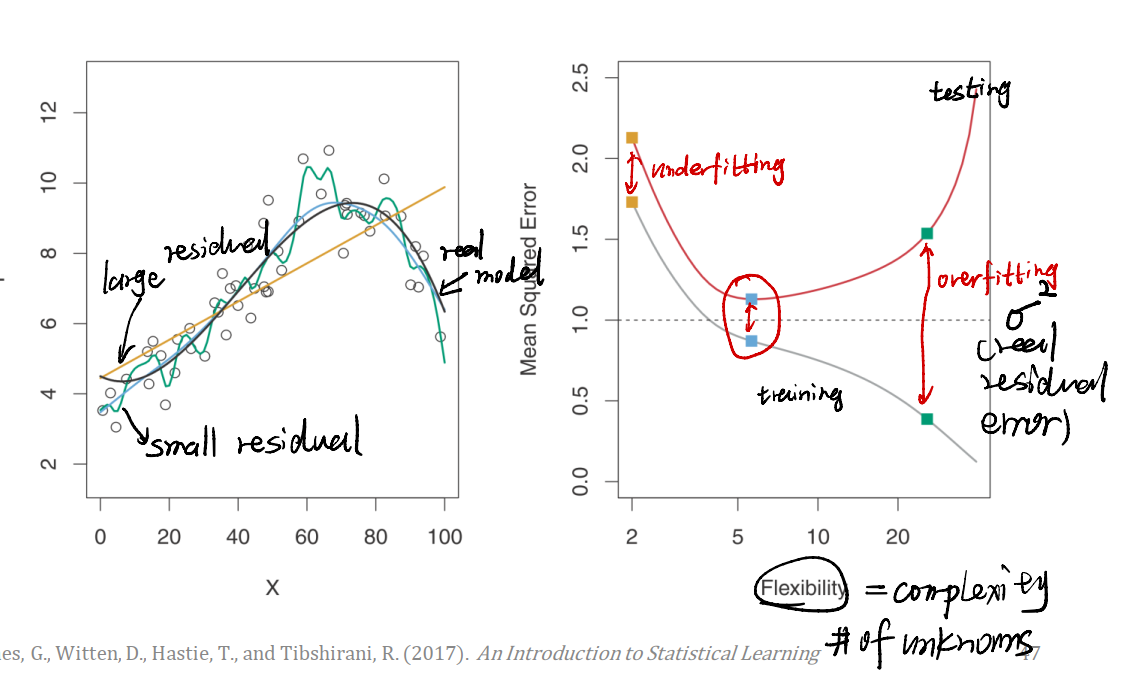
在上例左图中。黑色线是真实的模型，绿色线是一个相对复杂的模型，而蓝色线是一个相对简单的模型。我们给数据加上一个服从正态分布的噪声$\epsilon$，用以模拟真实情况。

• 绿色线虽然在一些数据点上表示良好，但是很显然，它并没有接近我们真实的模型，在一些地方与真实模型有很大的出入。
• 蓝色线虽然不能一一对应数据点，但是它更加接近真实模型。

右图给我们解释了这种情况：

• 模型简单的时候，训练和测试用数据集上的Mean Square Error很大，这个模型并没有拟合得多好，称为underfitting。
• 模型太复杂，在训练集上很强，但是测试集上很弱，这称为overfitting。
• 我们期望找到一个适合的状态。

Bias-Variance Tradeoff

我们经常要进行bias与variance之间的权衡。我们先来推导怎么刻画bias与variance。

从均方差开始：

\[E[(y - \hat{f})^2] = (f - E[\hat{f}])^2 + \sigma^2_\epsilon + V[\hat{f}]\]

均方差其实就是用真实数据$y$与我们模型预测得到的$\hat{f}$相减，平方加总起来取均值。

分解后得到三个部分，其中：

• 我们将$(f - E[\hat{f}])^2$称为Bias。$f$代表着the real model根据$x$算出的值，$E[\hat{f}]$是我们的模型算出值的期望。
  • 这样可以估测真实模型与我们通过回归得出模型之间的不同。
  • 这样的不同称为Bias。
  • 如果我们的模型与真实模型相差甚远，则会有较大的bias。
  • High bias can cause an algorithm to miss the relevant relations between features and target outputs。
• 我们将$V[\hat{f}]$称为Variance。
  • Variance衡量了我们的模型对不同数据集的敏感性。
  • High variance can cause an algorithm to model the random noise in the training data, rather than the intended outputs.
  • 在我们的模型中，测试集的随机性是我们所无法学习到的。当我们使用模型进行预测时，我们也没法处理它。
  • 一个模型有更多的param，那模型就有更高的敏感性，这可能非常危险。
  • 不过，复杂的模型也可能离真正的模型越近。
• $\sigma^2_\epsilon$称为nature noise，we can not get rid of it.

Reference

本文中的所有图片，Slides均来源于國立台灣大學工業工程學研究所藍俊宏副教授所開設的資料分析方法課程中之DA02 Regression Analysis.pdf。特此感謝老師在學習歷程上的幫助。